Баланс фондов в модели МОБ

Учёт баланса ОФ:

В этой модели вводится понятие фондоёмкости (капиталоёмкости):

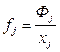- сколько фондов требуется для выпуска ед. продукции

Матрица прямой фондоёмкости: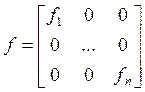

Баланс фондов: 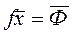- наличие фондов

Статический баланс с учётом ОПФ:

()

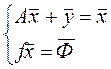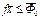Матрица коэффициентов полной фондоёмкости:

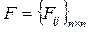- сколько фондов, созданных в отрасли i необходимо для выпуска ед. продукции в отрасли j с учётом прямых и косвенных связей.

; ;

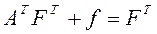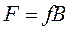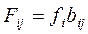
f_i – прямая фондоёмкость Fij – полная фондоёмкость

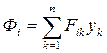- фонды в i-ой отр.

Объём фондов в i-ой отрасли должна быть = полной фондоёмкости всех конечных продуктов по данному виду фондов.

Динамические межотраслевые модели экономического роста. Динамическая и оптимизационная модели МОБ. Магистральные модели. Модель Гейла. Модель расширяющейся экономики Неймана. Модель МОБ, как частный случай модели Неймана. Магистральная модель накопления.

3.2. Динамические Модели МОБ:

В динамических моделях учитывается воспроизводство фондов за счёт инвестиций. Временной лаг =1.

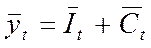- конечный продукт идёт на инвестиции и потребление

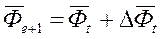- фонды в следующем году

Матрица А учитывает амортизацию

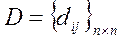- коэффициенты приростной капиталоёмкости

d_ij – объём инвестиций i-го вида или количество продукции i-го вида, который необходим для прироста фондов в j-ой отрасли.

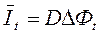
Матрица коэффициентов прямой трудоёмкости:

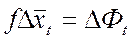
f- матрица прямой фондоёмкости

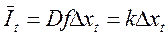; K=Df;

k_ij – коэффициент капитальных затрат – это объём капитального блага, созданного в i-ой отрасли, который используется в отрасли j для производства ед. продукции.

;

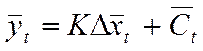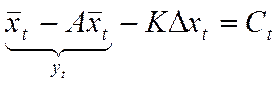
Траектория производного сектора экономики – изменение валового выпуска во времени. Траектория считается сбалансированной если выполнятся следующее соотношение: 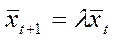, t= 1,2, λ>1

Объём фондов и конечные выпуски растут одинаковым темпом. Если матрица А продуктивна, то существует такое число λ>1, которое является темпом роста сбалансированной траектории развития производства.

3.3. Оптимизационные модели МОБ:

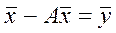
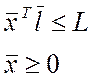
Оптимизация: произвести как можно больше стандартных наборов конечных продуктов. Структура конечного продукта задаётся: max α

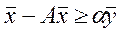
α –стандартных наборов

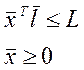
Оптимизация за счёт структуры валового выпуска

Двойственная задача:

min Lq

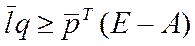
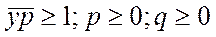
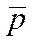- вектор двойственных оценок конечных продуктов.

Цены прямо пропорциональны затратам труда.

Постановка Джона фон Неймана

минимизация затрат труда при выполнении плана

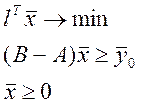
l^T – вектор прямых затрат труда

В – вектор интенсивности использования технологических способов.

Матрица В – выпуска

Матрица А – затрат.

Новожилов Виктор Викторович развивал эту модель.