Законы Кирхгофа в комплексной форме

Рис. 6.3. Векторная диаграмма для ветви с активным сопротивлением

Пусть к выводам ёмкости приложено гармоническое напряжение с комплексной амплитудой (6.18).

Напряжение и ток в ёмкости связаны между собой дифференциальным уравнением

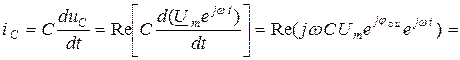
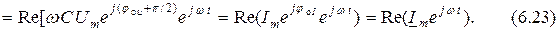
Отсюда по закону Ома (6.17) находим выражение комплексной амплитуды тока в ёмкости

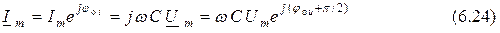
и, используя формулу (6.16), получаем выражение для сопротивления ёмкости в комплексной форме

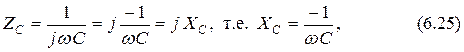
которое является чисто мнимой величиной.

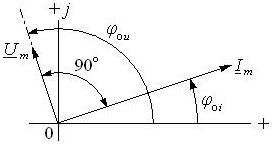
Из выражения (6.24) следует, что 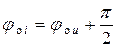, то есть ток в ёмкости опережает по фазе напряжение на 90^о (рис. 6.4).

Пусть через индуктивность протекает гармонический ток с комплексной амплитудой

Напряжение и ток в индуктивности связаны дифференциальным уравнением

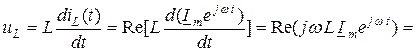
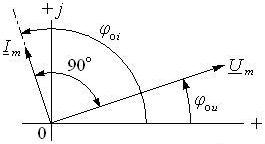
Рис. 6.4. Векторная диаграмма для ёмкости

Отсюда имеем уравнение закона Ома (6.17) применительно к индуктивности

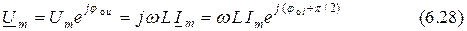
и, используя формулу (6.17), получаем выражение для сопротивления индуктивности в комплексной форме

которое является чисто мнимой положительной величиной.

Из уравнения (6.28) следует, что 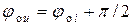, то есть фаза напряжения на индуктивности опережает ток на 90^о (рис. 6.5).

Предположим, что принципиальная электрическая схема цепи содержит 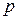ветвей и 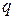узлов. При этом всегда выполняется условие .

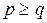Первый закон Кирхгофа относится к узлам электрической цепи и может быть сформулирован как:

– алгебраическая сумма токов в узле равна нулю

либо как:

– сумма втекающих в узел токов равна сумме вытекающих из него: