Схемы замещения контуров

Классификация контуров

Резонансы в связанных контурах

Схемы замещения контуров

Классификация контуров

СВЯЗАННЫЕ КОНТУРЫ

ЛЕКЦИЯ 17

План лекции:

Контуры, взаимно влияющие друг на друга, называют связанными.

Связанные контуры применяют для получения более прямоугольных, чем у одиночных контуров, амплитудно-частотных характеристик (АЧХ). При этом чем больше связанных контуров в системе, тем форма АЧХ ближе к прямоугольной.

Простейшими являются системы из двух связанных контуров (рис. 17.1). Систему из трёх и более связанных контуров часто называют фильтрами сосредоточенной селекции

Классификация контуров по виду связи приведена в подрисуночной под­писи. Элемент схемы, принадлежащий одновременно обоим контурам, называют элементом связи. Гальваническую связь (рис. 17.1, д), то есть связь с помощью активного сопротивления – резистора, применяют редко. Другие активные сопротивления в схемах являются сопротивлениями потерь и в виде отдельных дискретных элементов в цепи отсутствуют. Остальные виды связи являются реактивными.

В системе связанных контуров контуры могут быть колебательными или апериодическими независимо друг от друга.

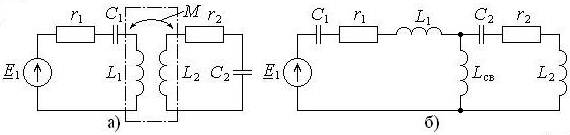
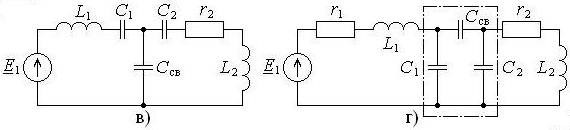
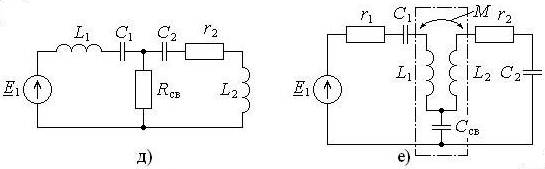
Рис. 17.1. Системы из двух связанных контуров (а – трансформаторная связь, б - автотрансформаторная связь, в – внутренняя ёмкостная связь, г – внешняя ёмкостная связь, д – гальваническая связь, е – комбинированная связь)

В последнее время вместо контуров с сосредоточенными элементами 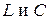стали успешно применять твёрдотельные контуры, выполненные, например, на пьезопластинах с использованием поверхностных акустических волн.

С целью создания общей теории расчёта, пригодной для любых типов связанных контуров и любого вида связи, заменим Т-образной схемой замещения (рис. 17.2 – штриховая линия) четырёхполюсники, обведённые на рис. 17.1 штрихпунктирными линиями. У остальных разновидностей связанных контуров элементы связи и без преобразования образуют Т-образное соединение.

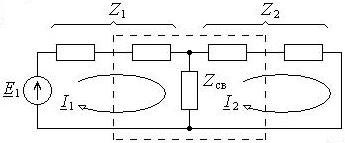
Рис. 17.2. Обобщённая схема системы двух связанных контуров

На рисунке 17.2 через 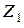обозначено сопротивление, принадлежащее только первому контуру, 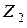– сопротивление, принадлежащее только второму контуру, 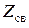– сопротивление связи, принадлежащее обоим контурам, 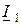и 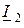– контурные токи первого и второго контуров соответственно.

Составим уравнения по второму закону Кирхгофа:

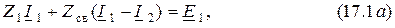
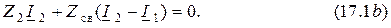
Обозначим через 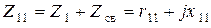полное или собственное сопротивление первого контура, через 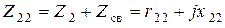– полное или собственное сопротивление второго. Для нахождения сопротивления 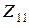следует разомкнуть цепь, в которой протекает ток 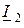, а для нахождения 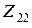– цепь, в которой протекает ток .

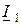Частоту 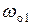, на которой выполняется условие 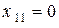, называют собственной резонансной частотой первого контура, частоту 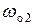, на которой выполняется условие 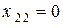, – собственной резонансной частотой второго контура.

Уравнения (17.1) можно привести к виду

Используя уравнение 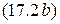, выразим ток 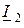через ток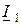

Заменяя ток 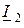в формуле 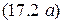через ток 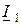, находим выражение контурного тока

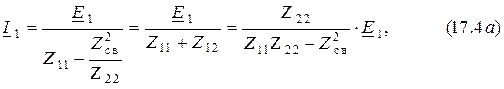
подставив которое в формулу (17.3), находим выражение второго контурного тока

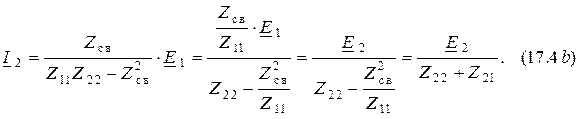
Уравнению 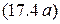соответствует эквивалентная схема замещения пер­вого контура (рис. 17.3, а), где 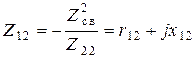называют вносимым сопротивлением в первый контур со стороны второго.

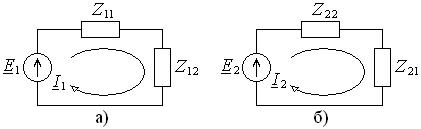
Рис. 17.3. Схемы замещения связанных контуров (а – первого, б - второго контура)

Уравнению 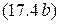соответствует эквивалентная схема замещения второго контура (рис. 17.3, б), в которой 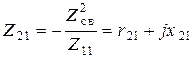– вносимое сопротивление, а 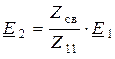– вносимая эдс во второй контур со стороны первого.

Вносимые сопротивления и вносимая эдс позволяют учесть влияние одного контура на другой из-за наличия связи между ними.

Допустим, что связь между контурами осуществляется с помощью реактивного элемента, то есть выполняется равенство .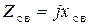

В этом случае вносимые сопротивления могут быть преобразованы к виду

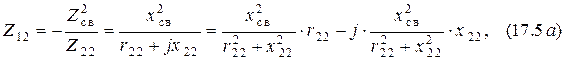
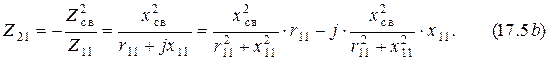
Следовательно, знаки собственного и вносимого от данного контура реактивного сопротивления противоположны, то есть контур, имеющий на данной частоте индуктивный характер, вносит в связанный с ним контур ёмкостное сопротивление и наоборот.