Коэффициенты связи
Амплитудно-частотные характеристики связанных контуров
ЛЕКЦИЯ 18
План лекции:
18.1. Коэффициенты связи [1]
Для количественной оценки взаимного влияния контуров вводят понятие коэффициента связи 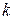 как среднего геометрического из коэффициентов связи первого контура со вторым
как среднего геометрического из коэффициентов связи первого контура со вторым  и второго контура с первым
и второго контура с первым 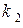 :
:

Коэффициентом связи первого контура со вторым называют отношение эдс, наведённой во втором контуре со стороны первого, к напряжению на всём элементе первого контура, наводящем эдс.
Коэффициентом связи второго контура с первым называют отношение эдс, наведённой в первом контуре со стороны второго, к напряжению на всём элементе второго контура, создающем эдс.
Для определения наводимой эдс необходимо разомкнуть контур, в который она наводится.
Согласно определениям получим конкретные выражения коэффициентов связи.
1. Трансформаторная связь (рис. 17.1а и рис. 13.2):
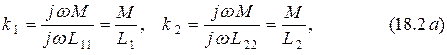

2. Автотрансформаторная связь (рис. 17.1, б):
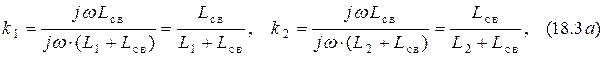
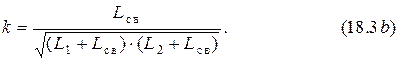
3. Внутренняя ёмкостная связь (рис. 17.1, в):
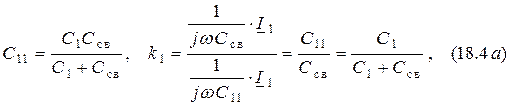
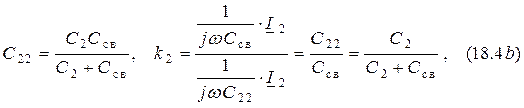
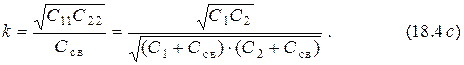
4. Внешняя ёмкостная связь (рис. 17.1, г).
Напряжение на ёмкости 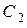 разомкнутого второго контура представляет собой наведённую в контур эдс
разомкнутого второго контура представляет собой наведённую в контур эдс 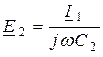 . Наводящей эдс является напряжение на ёмкости
. Наводящей эдс является напряжение на ёмкости 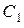 или, что то же самое, на цепи из последовательно соединённых емкостей
или, что то же самое, на цепи из последовательно соединённых емкостей 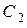 и
и  :
: 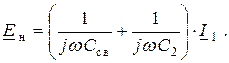
Поэтому 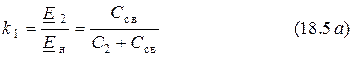
и аналогично  .
.
Отсюда имеем выражение для коэффициента связи
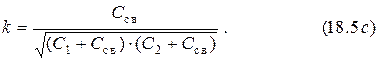
Эти формулы также можно получить, преобразуя соединение емкостей треугольником в соединение звездой (рис. 18.1) и используя формулы (6.8) и (6.14). После подстановки конкретных выражений емкостных сопротивлений схемы с внешней связью в вышеуказанные формулы и их преобразования получаем
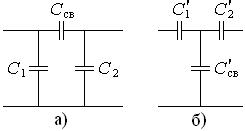
Рис. 18.1. Преобразование внешней ёмкостной связи (а) во внутреннюю (б)

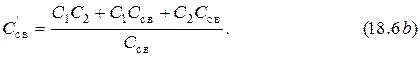
Формулы (18.4) и (18.6) позволяют найти величины собственных емкостей контуров с внешней ёмкостной связью
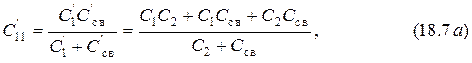

и коэффициенты связи, выражения которых совпадают с формулами (18.5).
Из полученных выше выражений (18.2) ÷ (18.5) следует, что коэффициенты связи есть постоянные величины.
В некоторых случаях, когда оба контура настроены на одну и ту же частоту, то есть выполняются условия полного резонанса 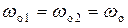 , коэффициенты связи бывает удобно выразить через такие вторичные параметры контуров как
, коэффициенты связи бывает удобно выразить через такие вторичные параметры контуров как  – сопротивление связи на частоте полного резонанса и характеристические сопротивления
– сопротивление связи на частоте полного резонанса и характеристические сопротивления 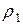 и
и  .
.
Получим соответствующие формулы.
1. Трансформаторная связь
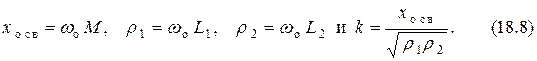
2. Автотрансформаторная связь
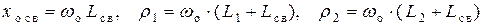

3. Внутренняя ёмкостная связь

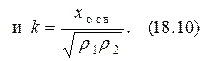
4. Внешняя ёмкостная связь
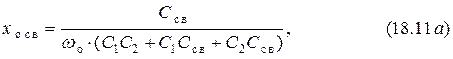
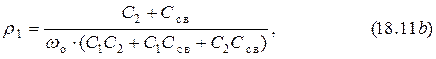


 2014-02-09
2014-02-09 1414
1414








