В системе связанных контуров при изменении параметров схемы или при изменении частоты входной эдс могут иметь место резонансы.
Если резонанс наступает в схеме замещения первого контура на некоторой частоте 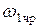 , то такое явление называют первым частным резонансом. Для него выполняются условия
, то такое явление называют первым частным резонансом. Для него выполняются условия
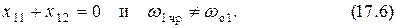
Поэтому 
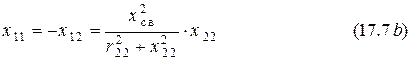
и 
Первый частный резонанс имеет место при одинаковом характере реактивных составляющих сопротивлений контуров. Ток первого контура при этом максимален.
Ток второго контура согласно формулам (17.3) и 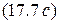 равен
равен
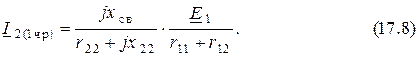
и в соответствии с равенством (17.3) также максимален
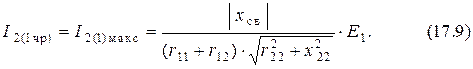
Если резонанс наступает в схеме замещения второго контура на некоторой частоте 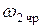 , то такое явление называют вторым частным резонансом, и для него выполняются аналогичные (17.6) условия
, то такое явление называют вторым частным резонансом, и для него выполняются аналогичные (17.6) условия
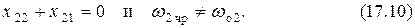
Отсюда 
и 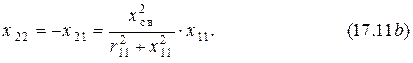
Ток второго контура при втором частном резонансе согласно формулам 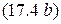 ,
, 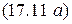 и определению вносимой эдс максимален и равен
и определению вносимой эдс максимален и равен
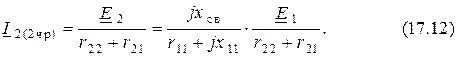
Величина этого тока будет равна
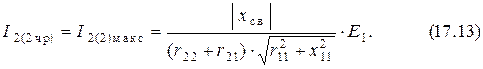
Если первый и второй контуры по отдельности настроены в резонанс на одну и ту же частоту, то имеет место полный резонанс и выполняются равенства 
При полном резонансе одновременно имеют место первый и второй частные резонансы, то есть 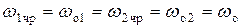 , так как согласно формулам (17.6) и (17.10) реактивные составляющие вносимых сопротивлений становятся равными нулю и выполняются условия
, так как согласно формулам (17.6) и (17.10) реактивные составляющие вносимых сопротивлений становятся равными нулю и выполняются условия 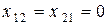 .
.
Поэтому амплитуда тока второго контура при полном резонансе будет наибольшей из максимальных (17.9) и (17.13) и равна
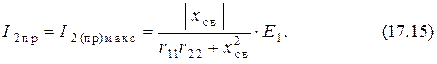
Если в системе связанных контуров имеет место первый частный резонанс (17.6) и выполняется условие
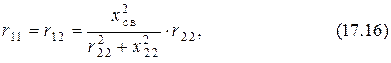
то такой резонанс называют оптимальным или сложным.
Преобразуем для него действительную часть вносимого сопротивления 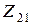 во второй контур со стороны первого, заменяя в формуле
во второй контур со стороны первого, заменяя в формуле  выражения
выражения  и
и 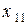 на (17.16) и
на (17.16) и 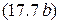 соответственно:
соответственно:
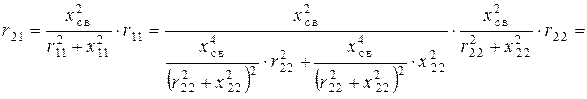
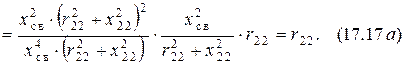
Преобразуя аналогичным образом мнимую часть вносимого сопротивления 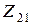 , получим уравнение
, получим уравнение
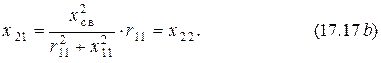
Следовательно, если при первом частном резонансе выполняется условие (17.16), то одновременно имеет место второй частный резонанс, то есть в системе связанных контуров имеет место полный резонанс.
Найдём условия, при которых наибольший ток второго контура (17.15) будет максимальным. Так как в выражении (17.15) единственной переменной является реактивное сопротивление связи, то приравняем нулю производную по этому параметру:
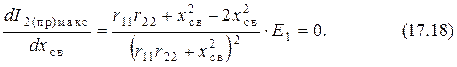
Отсюда получаем искомое условие 
и максимальную величину наибольшего тока во втором контуре
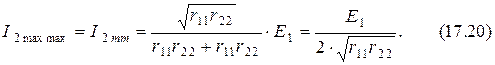
 2014-02-09
2014-02-09 4111
4111








