6.2.1. Модели матричных игр и их решение в чистых стратегиях. Рассмотрим парную игру (игру двух лиц), в которой у каждого из двух игроков А и В конечное число чистых стратегий.
Пусть игрок А располагает m чистыми стратегиями 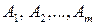 , а игрок В – n чистыми стратегиями
, а игрок В – n чистыми стратегиями 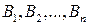 . Чтобы игра была полностью определенной, необходимо указать правило, сопоставляющее каждой паре чистых стратегий
. Чтобы игра была полностью определенной, необходимо указать правило, сопоставляющее каждой паре чистых стратегий 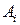 и
и 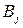 число
число 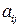 – выигрыш игрока А за счет игрока В или проигрыш игрока В. Если
– выигрыш игрока А за счет игрока В или проигрыш игрока В. Если 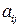 < 0, то игрок А платит игроку В сумму
< 0, то игрок А платит игроку В сумму 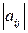 . Если игра состоит только из личных ходов (личный ход – игрок сознательно выбирает и реализует ту или иную стратегию), то выбор пары чистых стратегий (
. Если игра состоит только из личных ходов (личный ход – игрок сознательно выбирает и реализует ту или иную стратегию), то выбор пары чистых стратегий (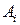 ;
;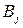 ) единственным образом определяет исход игры. Если же в игре используются и случайные ходы (выбор хода случаен), то исход игры обусловлен средним значением выигрыша (математическим ожиданием).
) единственным образом определяет исход игры. Если же в игре используются и случайные ходы (выбор хода случаен), то исход игры обусловлен средним значением выигрыша (математическим ожиданием).
Описанная выше игра является парной игрой с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого.
Если известны значения 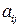 выигрыша для каждой пары (
выигрыша для каждой пары (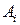 ;
;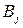 ) стратегий, то можно составить матрицу игры – платежную матрицу (таблица 6.1). Таблица 6.1
) стратегий, то можно составить матрицу игры – платежную матрицу (таблица 6.1). Таблица 6.1
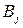 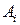 | 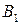 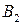 … … 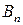 |
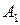 | 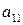 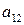 … … 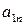 |
| … | … … … |
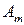 | 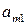 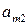 … … 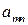 |
Платежная матрица – это табличная запись функции выигрыша. Игра с платежной матрицей называется матричной или прямоугольной.
Отдельная партия в такой игре реализуется следующим образом: игрок А выбирает одну из своих чистых стратегий – одну из строк платежной матрицы. Не зная результата его выбора, игрок В выбирает один из столбцов – свою чистую стратегию. Элемент матрицы, стоящий на пересечении выбранных строки и столбца, определяет выигрыш игрока А (проигрыш игрока В).
Цель игроков – выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В минимальный проигрыш. Считается, что каждый игрок считает своего противника разумным и стремящимся помешать ему достичь наилучшего результата.
Стратегия игрока А называется оптимальной, если при ее применении выигрыш игрока А не уменьшается, какими бы стратегиями ни пользовался игрок В. Стратегия игрока В называется оптимальной, если при ее применении проигрыш игрока В не увеличивается, какие бы стратегии ни применял игрок А. С учетом этого игрок А анализирует матрицу выигрышей следующим образом: для каждой своей чистой стратегии 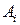 он определяет минимальное значение
он определяет минимальное значение 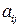 выигрыша не зависимо от применяемых игроком В чистых стратегий
выигрыша не зависимо от применяемых игроком В чистых стратегий 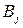 , т. е.
, т. е. 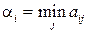 . Затем по минимальным выигрышам
. Затем по минимальным выигрышам 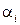 он отыскивает такую чистую стратегию
он отыскивает такую чистую стратегию 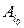 , при которой этот минимальный выигрыш будет максимальным:
, при которой этот минимальный выигрыш будет максимальным:
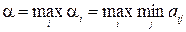 (6.1)
(6.1)
Число α, определяемое по формуле (6.1) называется нижней чистой ценой игры (максимином), и показывает, какой минимальный выигрыш может получить игрок А, применяя свои чистые стратегии при любых действиях игрока В. Соответствующая стратегия А 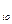 игрока А называется максиминной.
игрока А называется максиминной.
Игрок В старается уменьшить проигрыш, поэтому для каждой чистой стратегии 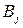 он отыскивает
он отыскивает 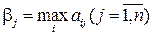 , а затем по
, а затем по 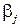 находит такую свою стратегию
находит такую свою стратегию 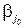 , при которой его проигрыш будет минимальным:
, при которой его проигрыш будет минимальным:
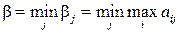 (6.2)
(6.2)
Число β называется верхней чистой ценой игры (минимаксом) и показывает, какой максимальный проигрыш, вследствие использования чистых стратегий, может быть у игрока В. Соответствующая стратегия 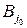 называется минимаксной.
называется минимаксной.
Таблица 6.2
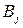 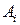 | 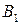 | 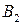 | … | 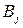 | … | 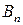 | 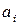 |
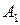 | 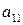 | 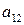 | … | 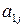 | … | 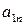 | 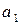 |
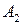 | 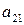 | 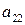 | … | 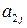 | … | 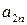 | 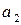 |
| … | … | … | … | … | … | … | |
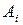 | 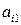 | 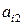 | … | 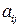 | … | 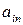 | 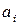 |
| … | … | … | … | … | … | … | … |
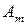 | 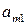 | 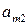 | … | 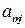 | … | 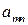 | 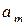 |
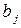 | 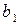 | 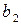 | … | 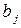 | … | 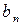 | 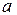 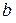 |
Таким образом, игрок А обеспечивает выигрыш не менее α, а игрок В может не позволить игроку А выиграть больше, чем β.
Принцип осторожности диктует игрокам выбор максиминной 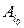 и минимаксной
и минимаксной 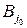 стратегий.
стратегий.
Теорема 6.1. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры:
α ≤ β.
Действительно, так как 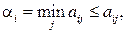 а
а 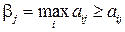 , то
, то 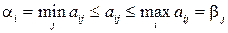 , т. е.
, т. е. 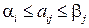 , тогда
, тогда 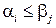 для любых
для любых 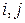 . Следовательно,
. Следовательно, 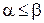 .
.
Если в матричной игре нижняя и верхняя чистые цены игры совпадают (т. е. α = β), то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры v = α = β.
Пара чистых стратегий (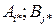 ) игроков А и В, при которых α = β, называется седловой точкой матричной игры, а элемент
) игроков А и В, при которых α = β, называется седловой точкой матричной игры, а элемент 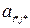 матрицы, стоящий на пересечении
матрицы, стоящий на пересечении 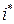 -строки и
-строки и 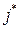 -столбца, – седловым элементом платежной матрицы.
-столбца, – седловым элементом платежной матрицы.
Седловой элемент 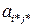 является наименьшим в
является наименьшим в 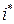 строке и наибольшим в
строке и наибольшим в 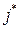 столбце, т. е.:
столбце, т. е.:  ≤
≤ 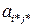 ≤
≤ 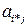 .
.
Поэтому, если игрок А отклонится от своей максиминной стратегии, то это приведет к уменьшению выигрыша. Если игрок В отклонится от своей минимаксной стратегии, то его проигрыш может возрасти. Следовательно, если в матричной игре есть седловой элемент, то наилучшими стратегиями для игроков являются их минимаксные стратегии: 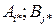 , которые называются оптимальными чистыми стратегиями игроков А и В, а решением игры является тройка
, которые называются оптимальными чистыми стратегиями игроков А и В, а решением игры является тройка 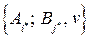 .
.
Пример 6.1. Найти максиминную и минимаксную стратегии в игре с матрицей
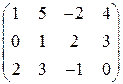 .
.
Решение. Составим платежную матрицу
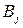 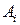 | 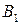 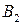 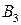 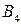 | 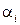 |
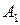 | 1 5 –2 4 | –2 |
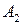 | 0 1 2 3 | |
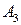 | 2 3 –1 0 | –1 |
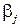 | 2 5 2 4 |
и выпишем в последнем столбце минимальные по строкам элементы 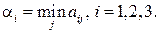
Наибольшим из них является 0, т. е. 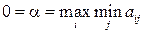 , значит, максиминной чистой стратегией игрока А является
, значит, максиминной чистой стратегией игрока А является 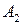 .
.
В последней строке таблицы приведены максимальные элементы соответствующих столбцов  . Наименьшим из них является 2, значит, минимакс:
. Наименьшим из них является 2, значит, минимакс:
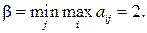
Минимаксной для игрока В является стратегия 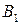 или
или 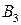 .
.
Седловой точки игра не имеет, т. е. игра не имеет оптимальных чистых стратегий и она не имеет чистой цены игры. Решение игры затрудняется.
Пример 6.2. Фирмы 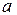 и
и 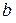 производят одинаковую сезонную продукцию, которая пользуется спросом в течение 3 месяцев. Доход от продажи продукции за месяц равен 20 ден. ед. Фирма
производят одинаковую сезонную продукцию, которая пользуется спросом в течение 3 месяцев. Доход от продажи продукции за месяц равен 20 ден. ед. Фирма 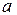 стремится вытеснить фирму
стремится вытеснить фирму 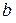 с рынка, способствуя минимизации ее дохода, путем повышения качества продукции и своевременной ее поставкой. Более качественная продукция пользуется большим спросом. Повышение качества требует дополнительных затрат и времени. Поэтому будем предполагать, что качество продукции тем выше, чем позже она поступает на рынок. Придать описанной ситуации игровую схему и построить платежную матрицу.
с рынка, способствуя минимизации ее дохода, путем повышения качества продукции и своевременной ее поставкой. Более качественная продукция пользуется большим спросом. Повышение качества требует дополнительных затрат и времени. Поэтому будем предполагать, что качество продукции тем выше, чем позже она поступает на рынок. Придать описанной ситуации игровую схему и построить платежную матрицу.
Решение. Примем фирмы 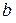 и
и 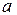 за игроков
за игроков  и
и 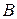 соответственно. Чистые стратегии
соответственно. Чистые стратегии 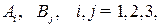 игроков
игроков  и
и 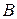 , состоят в том, что игрок
, состоят в том, что игрок  поставляет свою продукцию в момент времени
поставляет свою продукцию в момент времени 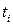 , а игрок
, а игрок 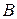 поставляет свою продукцию в момент времени
поставляет свою продукцию в момент времени 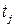 . Игрок
. Игрок  , поставляя свою продукцию в момент времени
, поставляя свою продукцию в момент времени 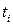 , стремится максимизировать свой доход, а игрок
, стремится максимизировать свой доход, а игрок 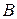 , выбирая момент времени поставки продукции
, выбирая момент времени поставки продукции 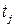 , стремится минимизировать доход игрока
, стремится минимизировать доход игрока  . Выигрыши
. Выигрыши 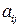 игрока
игрока  - это доходы фирмы
- это доходы фирмы 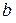 , которые находим используя условие задачи.
, которые находим используя условие задачи.
Из условия задачи следует, что если фирма 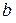 поставит свою продукцию на рынок в момент времени
поставит свою продукцию на рынок в момент времени 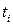 , а фирма
, а фирма 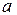 в момент
в момент 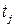 ,
, 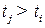 , то фирма
, то фирма 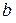 (игрок
(игрок  ), не имея конкурента в течение времени
), не имея конкурента в течение времени 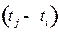 , получит за это время доход равный: 20
, получит за это время доход равный: 20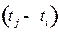 ден. ед. В момент
ден. ед. В момент 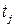 на рынке появляется продукция фирмы
на рынке появляется продукция фирмы 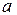 более высокого качества (см. условие, так как
более высокого качества (см. условие, так как 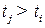 ) и фирма
) и фирма 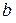 теряет доход.
теряет доход.
Если 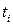 >
> 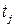 , то фирма
, то фирма 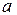 , предлагая товар более высокого качества, будет единолично получать доход от
, предлагая товар более высокого качества, будет единолично получать доход от 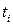 до истечения 3 месяцев. Доход фирмы
до истечения 3 месяцев. Доход фирмы 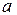 (игрок
(игрок 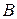 ) за это время будет равен: 20(3 -
) за это время будет равен: 20(3 - 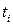 +1) ден.ед.
+1) ден.ед.
Если 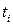 =
= 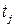 , т. е. продукция поступает одновременно от обеих фирм, то он реализуется с одинаковы спросом. Доход фирмы
, т. е. продукция поступает одновременно от обеих фирм, то он реализуется с одинаковы спросом. Доход фирмы 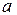 будет равен доходу фирмы
будет равен доходу фирмы 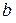 и составит: 10(3 -
и составит: 10(3 - 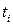 + 1) ден.ед.
+ 1) ден.ед.
Тогда выигрыши 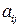 игрока
игрока  можно записать в виде следующей функции:
можно записать в виде следующей функции:
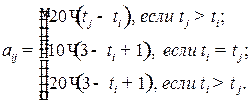 Воспользовавшись функцией выигрыша игрока
Воспользовавшись функцией выигрыша игрока  , платежную матрицу запишем в виде следующей таблицы 6.3.
, платежную матрицу запишем в виде следующей таблицы 6.3.
Таблица 6.3
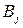 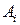 | 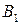 | 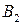 | 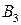 | 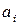 |
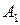 | ||||
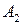 | ||||
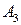 | ||||
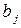 |
Определим нижние и верхние чистые цены игры (табл. 6.3):
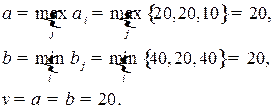
В данном случае имеем две седловые точки 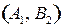 или
или 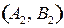 , а седловой элемент равен 20.
, а седловой элемент равен 20.
Таким образом, фирма 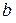 должна поставлять свою продукцию в первый и второй месяцы сезона, а фирма
должна поставлять свою продукцию в первый и второй месяцы сезона, а фирма 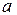 во второй месяц. Тогда максимальный доход фирмы
во второй месяц. Тогда максимальный доход фирмы 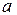 составит 20 ден. ед., а потери фирмы
составит 20 ден. ед., а потери фирмы 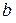 минимизируются и составят 20 ден. ед.
минимизируются и составят 20 ден. ед.
6.2.2. Модели матричных игр со смешанными стратегиями игроков. Свойства смешанных стратегий. Рассмотрим матричную игру:
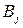 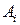 | 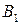 | 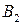 | … | 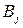 | … | 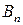 | 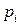 |
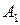 | 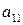 | 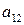 | … | 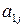 | 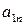 | 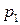 | |
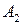 | 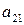 | 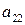 | … | 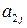 | … | 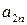 | 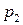 |
| … | … | … | … | … | … | … | … |
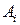 | 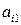 | 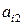 | … | 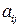 | … | 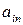 | 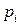 |
| … | … | … | … | … | … | … | … |
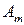 | 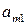 | 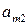 | … | 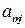 | … | 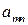 | 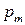 |
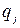 | 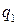 | 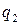 | … | 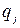 | … | 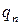 |
Обозначим через 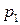 ,…,
,…, 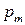 вероятности, с которыми игрок А использует чистые стратегии
вероятности, с которыми игрок А использует чистые стратегии 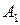 , …,
, …, 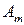 . В силу свойств вероятностей:
. В силу свойств вероятностей:
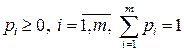 . (6.3)
. (6.3)
Упорядоченное множество р = (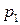 , …,
, …, 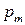 ), элементы которого удовлетворяют условиям (6.3), полностью определяют характер игры игрока А и называется его смешанной стратегией. Итак, смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. Множество смешанных стратегий определяется случайным выбором чистых стратегий. Любая его чистая стратегия А
), элементы которого удовлетворяют условиям (6.3), полностью определяют характер игры игрока А и называется его смешанной стратегией. Итак, смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. Множество смешанных стратегий определяется случайным выбором чистых стратегий. Любая его чистая стратегия А  может рассматриваться как частный случай смешанной стратегии, i -я компонента которой равна 1, а остальные равны нулю: р = (0; …; 1; …; 0).
может рассматриваться как частный случай смешанной стратегии, i -я компонента которой равна 1, а остальные равны нулю: р = (0; …; 1; …; 0).
Упорядоченное множество q = (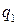 , …,
, …, 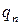 ), элементы которого удовлетворяют соотношениям
), элементы которого удовлетворяют соотношениям 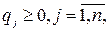
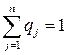 , называются смешанной стратегией игрока В.
, называются смешанной стратегией игрока В.
Применение смешанных стратегий p и q игроками А и В означает, что игрок А использует стратегию 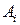 с вероятностью
с вероятностью 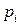 , а игрок В – стратегию
, а игрок В – стратегию 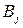 с вероятностью
с вероятностью 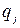 . Поскольку игроки выбирают свои стратегии случайно и независимо друг от друга, то вероятность выбора комбинации стратегий (
. Поскольку игроки выбирают свои стратегии случайно и независимо друг от друга, то вероятность выбора комбинации стратегий (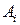 ,
, 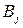 ) будет равна
) будет равна 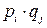 . При использовании смешанных стратегий игра приобретает случайный характер, поэтому случайными будут и выигрыши игрока А и проигрыши игрока В. Следовательно, можно вести речь лишь о средней величине (математическом ожидании) выигрыша (проигрыша). Эта величина является функцией смешанных стратегий p и q и определяется по формуле:
. При использовании смешанных стратегий игра приобретает случайный характер, поэтому случайными будут и выигрыши игрока А и проигрыши игрока В. Следовательно, можно вести речь лишь о средней величине (математическом ожидании) выигрыша (проигрыша). Эта величина является функцией смешанных стратегий p и q и определяется по формуле:
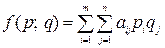 .
.
Функция f (p; q) называется платежной функцией игры с матрицей 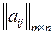 .
.
Смешанные стратегии 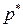 ,
, 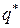 назовем оптимальными смешанными стратегиями игроков А и В, если они удовлетворяют неравенству:
назовем оптимальными смешанными стратегиями игроков А и В, если они удовлетворяют неравенству:
f (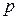 ,
, 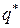 ) ≤ f (
) ≤ f (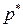 ,
, 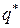 ) ≤ f (
) ≤ f (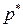 ,
, 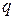 ) (6.4)
) (6.4)
для любых стратегий 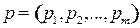 и
и 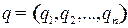 .
.
Значение f (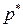 ,
, 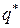 ) платежной функции при оптимальных стратегиях определяет цену игры v, т. е. v = f (
) платежной функции при оптимальных стратегиях определяет цену игры v, т. е. v = f (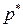 ,
, 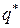 ).
).
В седловой точке 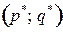 платежная функция
платежная функция 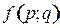 достигает максимума по смешанным стратегиям
достигает максимума по смешанным стратегиям 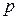 игрока
игрока  и минимума по смешанным стратегиям
и минимума по смешанным стратегиям 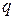 игрока
игрока 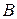 .
.
Рассмотрим игру с матрицей 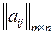 и предположим, что
и предположим, что 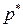 и
и 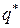 – оптимальные смешанные стратегии игроков и v = f (
– оптимальные смешанные стратегии игроков и v = f (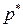 ,
, 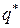 ) – цена игры. Проверку того, что набор (
) – цена игры. Проверку того, что набор (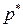 ,
, 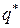 , v) является решением, можно провести при помощи теоремы 6.2.
, v) является решением, можно провести при помощи теоремы 6.2.
Теорема 6.2. Для того, чтобы смешанные стратегии 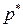 = (
= (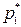 , …,
, …, 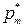 ) и
) и 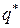 = = (
= = (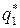 ,
, 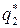 , …,
, …, 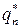 ), были оптимальными для игроков А и В в игре с матрицей
), были оптимальными для игроков А и В в игре с матрицей 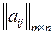 и ценой v, необходимо и достаточно выполнения неравенств:
и ценой v, необходимо и достаточно выполнения неравенств:
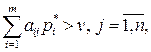
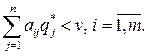
Кроме того, смешенные стратегии удовлетворяют еще следующим теоремам.
Теорема 6.3. В смешанных стратегиях любая конечная матричная игра имеет седловую точку.
Теорема 6.4. Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.
Активные стратегии – это чистые стратегии игрока, входящие в оптимальную смешанную стратегию с вероятностями, отличными от нуля.
Из теоремы 6.2 вытекает принципиальное решение матричной игры: надо найти неотрицательное решение (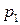 ,
, 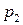 , …,
, …, 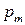 ,
, 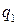 ,
, 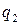 , …,
, …,  , v) системы
, v) системы 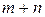 линейных неравенств и линейных уравнений:
линейных неравенств и линейных уравнений:
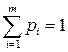 ;
; 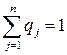 .
.
Отметим, что число активных стратегий игроков не превышает наименьшего из чисел m и n.
Решение матричной игры можно упростить, если воспользоваться доминированием одних стратегий над другими.
Говорят, что стратегия 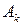 доминирует над стратегией
доминирует над стратегией 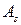 , если элементы k -й строки не меньше соответствующих элементов s -ой строки:
, если элементы k -й строки не меньше соответствующих элементов s -ой строки: 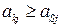 ,
, 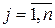 . Выигрыш игрока А в этом случае (при стратегии
. Выигрыш игрока А в этом случае (при стратегии 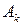 ) больше чем при стратегии
) больше чем при стратегии 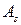 , какой бы стратегией не воспользовался игрок В. Стратегию
, какой бы стратегией не воспользовался игрок В. Стратегию 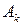 назовем доминирующей, а стратегию
назовем доминирующей, а стратегию 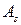 – доминируемой.
– доминируемой.
Аналогично и для столбцов:
если элементы l -го столбца не превосходят соответствующих элементов r -го столбца: 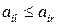 ,
, 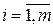 , то игроку В выгоднее применять стратегию
, то игроку В выгоднее применять стратегию  , чем
, чем 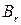 , так как он будет проигрывать меньше. Поэтому стратегия
, так как он будет проигрывать меньше. Поэтому стратегия  доминирует над стратегией
доминирует над стратегией 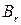 . Стратегия
. Стратегия  называется доминирующей, стратегия
называется доминирующей, стратегия 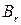 – доминируемой.
– доминируемой.
Если 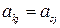 ,
, 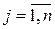 , или
, или 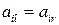 ,
, 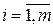 , то стратегии
, то стратегии 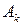 и
и 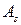 ,
,  и
и 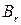 называются дублирующими.
называются дублирующими.
Пример 6.3. Выполнить возможные упрощения платежной матрицы:
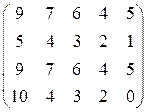
Решение. Элементы первой и третьей строки соответственно равны. Поэтому одну из них можно удалить. Элементы второй строки не превышают соответственно элементов первой строки, поэтому удаляем вторую строку и приходим к матрице
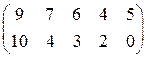
Элементы первого столбца преобразованной матрицы больше соответствующих элементов второго столбца, элементы второго столбца больше соответствующих элементов третьего столбца; элементы третьего столбца больше соответствующих элементов четвертого столбца. Поэтому доминируемые первый, второй и третий столбцы опускаем. В результате получаем матрицу
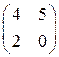 .
.
 2014-02-09
2014-02-09 2637
2637
