Решение моделей матричных игр сведением к паре взаимно двойственных линейных оптимизационных моделей. Выше установлено, что если игра имеет седловую точку, то решение ее лежит в области чистых стратегий: оптимальными будут максиминные (минимаксные) стратегии, а ценой игры – седловой элемент матрицы игры.
Оптимальные же смешанные стратегии для игр без седловых точек можно получить, решая систему 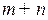 линейных неравенств:
линейных неравенств:
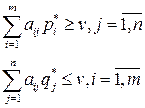
и линейных уравнений:
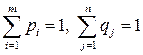 (
(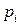 ≥ 0,
≥ 0, 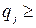 0).
0).
Этот путь нерационален, так как связан с большим объемом вычислений.
Покажем, что решение любой конечной матричной игры может быть сведено к решению линейной оптимизационной модели.
Пусть игра задана матрицей 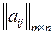 ,
, 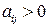 . Поскольку элементы платежной матрицы положительны, то и цена игры
. Поскольку элементы платежной матрицы положительны, то и цена игры 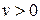 .
.
Найдем сначала оптимальную смешанную стратегию 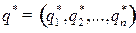 игрока В. Применяя ее, игрок В проиграет не более цены v, какую бы чистую стратегию
игрока В. Применяя ее, игрок В проиграет не более цены v, какую бы чистую стратегию 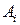 не применял игрок А, т. е.
не применял игрок А, т. е.
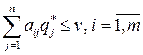 .
.
Разделим обе части неравенств на v, получим:
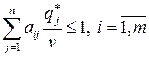 .
.
Обозначив
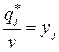 ,
, 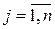 , (6.5)
, (6.5)
будем иметь:
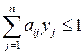 ,
, 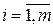 ,
,
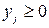 ,
, 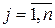 . (6.6)
. (6.6)
Кроме того, 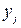 удовлетворяет условию:
удовлетворяет условию:
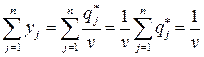 .
.
Игрок В стремится сделать свой проигрыш 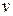 наименьшим, а, следовательно, будет возрастать величина
наименьшим, а, следовательно, будет возрастать величина
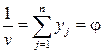 . (6.7)
. (6.7)
Учитывая выше сказанное, приходим к линейной оптимизационной модели, записанной в симметричной форме: максимизировать линейную функцию
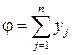
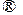 max, (6.8)
max, (6.8)
при линейных ограничениях:
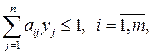 (6.9)
(6.9)
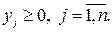 (6.10)
(6.10)
Решив ее, найдем оптимальный план 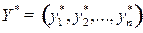 и
и 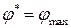 , а затем, используя (6.7) и (6.5), определим цену игры
, а затем, используя (6.7) и (6.5), определим цену игры 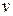 и компоненты оптимальной смешанной стратегии
и компоненты оптимальной смешанной стратегии 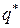 :
:
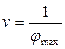 ,
, 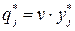 ,
, 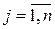 .
.
Аналогично можно построить еще одну линейную оптимизационную модель для определения оптимальной смешенной стратегии игрока  , рассмотрев неравенства
, рассмотрев неравенства
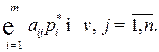
Минимизировать функцию:
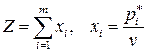 (6.11)
(6.11)
при ограничениях:
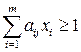 ,
, 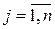 , (6.12)
, (6.12)
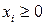 ,
, 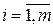 . (6.13)
. (6.13)
Решая ее, найдем оптимальный план: 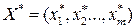 и
и 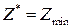 , а затем найдем цену, и оптимальную смешанную стратегию
, а затем найдем цену, и оптимальную смешанную стратегию 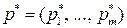 игрока А:
игрока А:
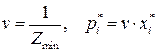 ,
, 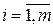 .
.
Модели (6.8)-(6.10) и (6.11)-(6.13) образуют пару двойственных линейных оптимизационных моделей.
Найдя решение одной из них, решение другой находим из строки целевой функции последней симплексной таблицы, воспользовавшись соответствием между переменными:
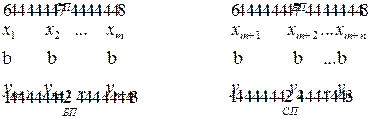
При решении матричных игр размерностью 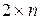 и
и 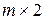 целесообразно использовать графический метод.
целесообразно использовать графический метод.
Пример 6.4. Найти решение игры с матрицей
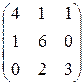 .
.
Решение. Найдем сначала оптимальную смешанную стратегию 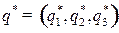 игрока В.
игрока В.
Для этого составим линейную оптимизационную модель: найти план 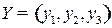 , при котором целевая функция
, при котором целевая функция
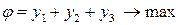 ,
,
и который удовлетворяет ограничениям:
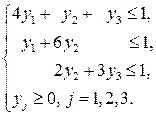
Эту модель решаем симплекс-методом. Сначала вводим неотрицательные вспомогательные переменные 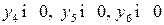 и приводим систему ограничений к предпочтительному виду:
и приводим систему ограничений к предпочтительному виду:
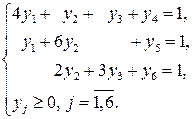
Составляем первую симплексную таблицу
| БП | 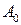
| СП | ||
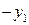
| 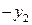
| 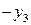
| ||
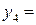
| 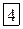
| |||
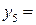
| ||||
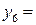
| ||||
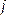
| –1 | –1 | –1 |
и находим решение в следующих симплексных таблицах:
| БП | 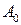
| СП | ||
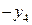
| 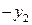
| 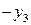
| ||
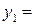
| 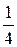
| 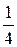
| 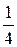
| 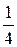
|
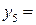
| 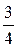
| 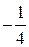
| 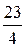
| 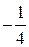
|
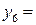
| 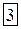
| |||
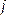
| 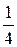
| 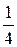
| 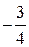
| 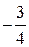
|
| БП | 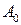
| СП | ||
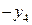
| 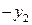
| 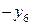
| ||
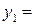
| 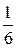
| 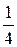
| 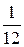
| 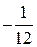
|
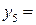
| 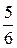
| 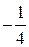
| 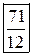
| 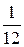
|
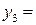
| 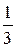
| 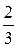
| 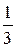
| |
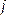
| 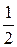
| 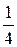
| 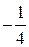
| 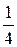
|
| БП | 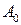
| СП | ||
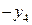
| 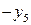
| 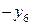
| ||
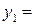
| 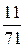
| 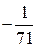
| ||
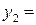
| 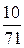
| 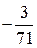
| 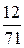
| 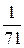
|
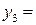
| 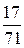
| 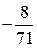
| ||
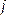
| 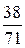
| 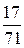
| 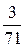
| 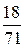
|
В последней симплексной таблице получено оптимальное решение: 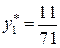 ,
, 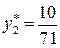 ,
, 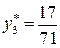 ,
, 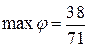 .
.
Цену игры и компоненты оптимальной смешанной стратегии 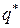 определим по формулам
определим по формулам 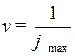 и
и 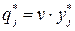 :
:
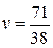 ,
, 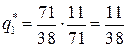 ,
, 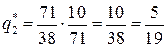 ,
, 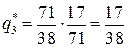 .
.
Таким образом, 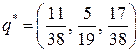 .
.
Аналогично строим модель для определения оптимальной смешанной стратегии игрока А.
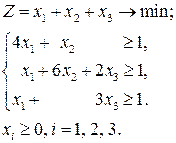
Преобразуем модель к каноническому виду, вычитая вспомогательные неотрицательные переменные 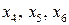 :
:
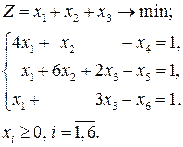
Решение этой модели находим, воспользовавшись соответствием между переменными исходной и двойственной моделей:
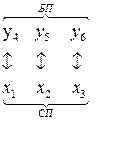
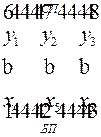
Оптимальное решение двойственной модели находим из последней симплексной таблицы, учитывая соответствие между переменными: 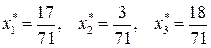 ,
, 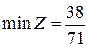 . Оптимальную смешанную стратегию игрока А определим по формулам:
. Оптимальную смешанную стратегию игрока А определим по формулам: 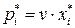 ,
, 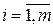 . Отсюда,
. Отсюда, 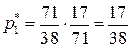 ,
, 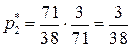 ,
, 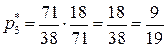 .
.
Таким образом, оптимальная смешенная стратегия игрока  имеет вид:
имеет вид: 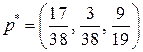 .
.
Пример 6.5. Два банка  и
и  выделяют денежные средства на финансирование трех проектов. С учетом особенностей вкладов и выдачи кредитов прибыль банка
выделяют денежные средства на финансирование трех проектов. С учетом особенностей вкладов и выдачи кредитов прибыль банка  в зависимости от объемов финансирования определяется элементами матрицы
в зависимости от объемов финансирования определяется элементами матрицы
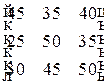 . Предположим, что потери банка
. Предположим, что потери банка  при этом равны прибыли банка
при этом равны прибыли банка  . Определить оптимальные смешанные стратегии банков
. Определить оптимальные смешанные стратегии банков  и
и  .
.
Решение. Предположим, что банк  располагает суммой в
располагает суммой в 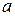 ден. ед., отпускаемой на финансирование трех проектов. Тогда чистая стратегия
ден. ед., отпускаемой на финансирование трех проектов. Тогда чистая стратегия 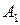 - это сумма в
- это сумма в 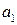 ден. ед. выделенная на финансирование первого проекта; чистая стратегия
ден. ед. выделенная на финансирование первого проекта; чистая стратегия 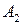 - это сумма в
- это сумма в 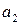 ден. ед. выделенная на финансирование второго проекта; чистая стратегия
ден. ед. выделенная на финансирование второго проекта; чистая стратегия 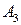 - это сумма в
- это сумма в 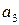 ден. ед. выделенная на финансирование третьего проекта. Банк
ден. ед. выделенная на финансирование третьего проекта. Банк 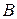 также располагает суммой в
также располагает суммой в 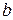 ден. ед., отпускаемой на финансирование трех проектов. Чистые стратегии
ден. ед., отпускаемой на финансирование трех проектов. Чистые стратегии 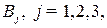 - это суммы в
- это суммы в 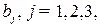 ден. ед., выделенные на финансирование трех проектов. Общие суммы средств, выделенных на финансирование трех проектов, удовлетворяют равенствам:
ден. ед., выделенные на финансирование трех проектов. Общие суммы средств, выделенных на финансирование трех проектов, удовлетворяют равенствам: 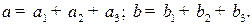
Решим игру в чистых стратегиях. Для этого составим платежную матрицу:
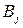
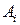
| 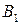
| 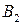
| 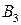
| 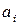
|
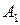
| ||||
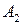
| ||||
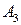
| ||||
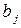
|
Из матрицы видим, что 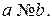 Следовательно, игра не имеет решения в чистых стратегиях. Поэтому решение игры найдем в смешенных стратегиях. Цена игры
Следовательно, игра не имеет решения в чистых стратегиях. Поэтому решение игры найдем в смешенных стратегиях. Цена игры 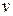 заключена между нижней
заключена между нижней 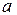 и верхней
и верхней 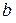 чистыми ценами, т.е.
чистыми ценами, т.е. 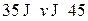 .
.
Составим математические модели для каждого игрока, предварительно упростив матрицу: разделим все элементы платежной матрицы на 5 и вычтем из полученных элементов 4. Получим матрицу 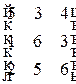 . Цена в упрощенной матичной игре будет равна:
. Цена в упрощенной матичной игре будет равна: 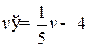 , где
, где 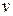 цена в исходной игре. С учетом упрощения математическая модель для игрока
цена в исходной игре. С учетом упрощения математическая модель для игрока  будет иметь вид:
будет иметь вид:
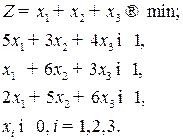
Для игрока 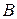 :
: 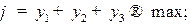
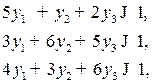
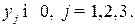
Преобразуем модели к канонической форме записи, вводя вспомогательные переменные 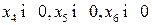 для исходной модели и
для исходной модели и 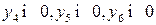 для двойственной модели. Введенные вспомогательные переменные примем за базисные переменные. Укажем соответствие между переменными пары взаимно двойственных моделей:
для двойственной модели. Введенные вспомогательные переменные примем за базисные переменные. Укажем соответствие между переменными пары взаимно двойственных моделей:
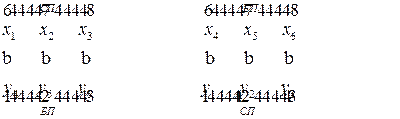
Решим двойственную модель симплексным методом. Каноническая форма записи этой модели имеет вид:
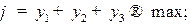
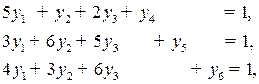
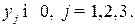
Составим симплексную таблицу:
| БП | 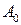
| СП | ||
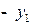
| 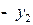
| 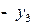
| ||
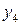
| 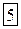
| |||
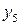
| ||||
| ||||
| -1 | -1 | -1 |
Последовательно преобразуем первоначальную симплексную таблицу:
| БП | 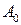
| СП | ||
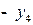
| 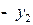
| 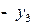
| ||
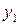
| 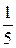
| 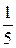
| 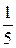
| 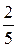
|
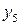
| 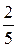
| 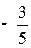
| 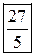
| 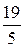
|
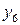
| 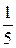
| 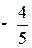
| 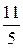
| 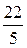
|
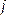
| 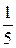
| 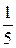
| 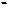 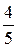
| 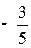
|
| БП | 
| СП | ||
| 
| 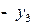
| ||
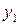
| 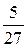
| 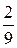
| 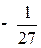
| 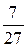
|
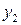
| 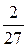
| 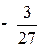
| 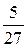
| 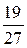
|
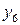
| 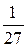
| 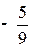
| 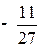
| 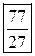
|
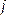
| 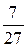
| 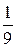
| 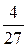
| 
|
| БП | 
| СП | ||
| 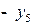
| 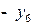
| ||
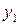
| 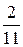
| |||
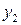
| 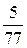
| |||
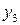
| 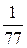
| |||
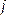
| 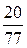
| 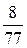
| 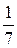
| 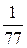
|
В последней симплексной таблице содержится оптимальный план: 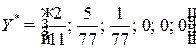 ;
; 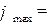
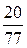 . Учитывая соответствие между переменными, находим оптимальный план игрока
. Учитывая соответствие между переменными, находим оптимальный план игрока  :
: 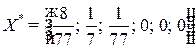 ;
; 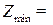
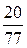 .
.
Применяя формулы 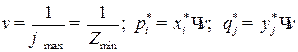 , находим цену игры и вероятности
, находим цену игры и вероятности 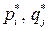 для оптимальных смешанных стратегий:
для оптимальных смешанных стратегий: 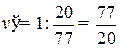 ;
; 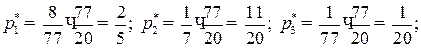
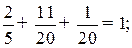
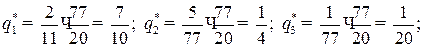
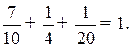
Таким образом, применяя свою смешанную стратегию 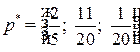 , банк
, банк  получит прибыль не менее
получит прибыль не менее 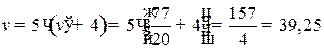 ден. ед.,
ден. ед.,
а убыток банка 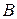 при применении своей смешанной стратегии
при применении своей смешанной стратегии 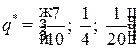 , составит не более 39,25 ден. ед.
, составит не более 39,25 ден. ед.
Следовательно, из общей суммы средств 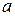 ден. ед., выделяемых банком
ден. ед., выделяемых банком  на финансирование трех проектов, на долю первого проекта должно выделяться 40%, второго – 55%, третьего – 5% этой суммы. Банк
на финансирование трех проектов, на долю первого проекта должно выделяться 40%, второго – 55%, третьего – 5% этой суммы. Банк 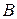 распределяет выделенные средства
распределяет выделенные средства 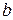 ден. ед. следующим образом: на финансирование первого проекта – 70%, второго – 25%, третьего – 5%. Такое распределение денежных средств банками
ден. ед. следующим образом: на финансирование первого проекта – 70%, второго – 25%, третьего – 5%. Такое распределение денежных средств банками  и
и 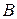 на финансирование трех проектов позволит им получить максимальную прибыль равную 39,25 ден. ед.
на финансирование трех проектов позволит им получить максимальную прибыль равную 39,25 ден. ед.
6.3.1.Общие понятия статистических игр. Изучая матричные игры, мы предполагали, что каждый из игроков (участников) стремится к наилучшему для себя результату. На практике же встречаются игры, ситуации, когда один из игроков безразличен к результату игры. Например, управление производственными процессами осуществляется путем реализации последовательности принимаемых решений. Для принятия эффективных решений необходима информация о состоянии объекта управления. С целью уменьшения неблагоприятных последствий в каждом конкретном случае следует учитывать степень риска. В приведенном примере, лицо (или группу лиц), принимающее решение, вступает в игровые отношения с некоторым абстрактным участником игры. В качестве такого игрока выступает «природа». Под природой понимается комплекс внешних обстоятельств (условий), при которых приходится принимать решение. В такой ситуации игрока (группу лиц, объединенных общностью цели) называют статистиком, а игры, в которых одним из участников является человек (игрок А), а другим природа (игрок 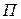 ), называются статистическими. Ясно, что природа развивается по объективным законам, независимо от человека, который не всегда знает или знает не полно эти законы. Поэтому, принимая решения, человек должен учитывать их последствия. Любую хозяйственную деятельность человека можно рассматривать как игру с природой.
), называются статистическими. Ясно, что природа развивается по объективным законам, независимо от человека, который не всегда знает или знает не полно эти законы. Поэтому, принимая решения, человек должен учитывать их последствия. Любую хозяйственную деятельность человека можно рассматривать как игру с природой.
Как и в матричных играх, игрок А может использовать стратегии 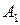 ,
, 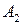 , …,
, …, 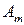 . Множество состояний природы
. Множество состояний природы 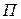 назовем множеством стратегий
назовем множеством стратегий 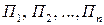 , имея в виду полную совокупность внешних условий, в которых статистику А приходится выбирать свою стратегию. Статистику А обычно известны возможности состояния природы
, имея в виду полную совокупность внешних условий, в которых статистику А приходится выбирать свою стратегию. Статистику А обычно известны возможности состояния природы 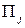 , а иногда вероятности
, а иногда вероятности 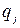 с которыми она реализует эти состояния. Эти вероятности называются априорными. Проводя эксперименты, статистик может уточнить состояния
с которыми она реализует эти состояния. Эти вероятности называются априорными. Проводя эксперименты, статистик может уточнить состояния 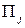 и их вероятности
и их вероятности 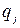 , которые называются апостериорными.
, которые называются апостериорными.
Мы рассмотрим статистические игры без эксперимента.
Статистик в своих взаимоотношениях с природой может пользоваться как чистыми стратегиями 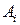 , так и смешанными:
, так и смешанными:
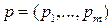 ,
, 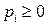 ,
, 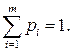
Если статистику А известны числа 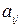 , характеризующие пару стратегий (
, характеризующие пару стратегий (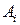 ,
, 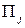 ), то статистическую игру можно задать платежной матрицей
), то статистическую игру можно задать платежной матрицей 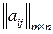 .
.
Пример 6.6. В фирме «Плюс» при производстве продукции потребляется 20-22 единицы сырья S, в зависимости от его качества. Если для выпуска запланированной продукции сырья окажется недостаточно, то запас его можно пополнить, но одна единица сырья при этом будет стоить 10 ден. ед. Если же запас сырья будет большим, то на хранение и содержание единицы сырья нужно затратить 7 ден.ед.
Придадим описанной ситуации игровую схему. В качестве статистика (игрок А) выступает администрация предприятия, которая может заказать 20, 21 или 22 единицы сырья (стратегии 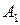 ,
, 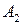 ,
, 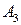 ). Вторым игроком (природа
). Вторым игроком (природа 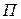 ) может выступать фактический расход сырья в процессе производства. Расход сырья зависит от качества сырья и составляет 20, 21 или 22 единицы сырья (состояния природы
) может выступать фактический расход сырья в процессе производства. Расход сырья зависит от качества сырья и составляет 20, 21 или 22 единицы сырья (состояния природы 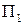 ,
, 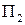 ,
, 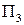 ). Элементы матрицы
). Элементы матрицы 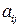 характеризуют дополнительные затраты, вызванные доставкой сырья в случае недостатка или хранением в случае избытка.
характеризуют дополнительные затраты, вызванные доставкой сырья в случае недостатка или хранением в случае избытка.
Паре стратегий (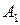 ,
, 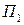 ) соответствует число
) соответствует число 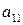 = 0, так как расход и закупка сырья равны.
= 0, так как расход и закупка сырья равны.
Паре стратегий (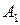 ,
, 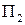 ) соответствует число
) соответствует число 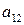 = –10, так как расход превысит запасы и нужно закупить одну единицу сырья.
= –10, так как расход превысит запасы и нужно закупить одну единицу сырья.
Паре стратегий (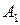 ,
, 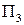 ) соответствует число
) соответствует число 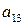 = –20, закупить нужно 2 единицы сырья.
= –20, закупить нужно 2 единицы сырья.
Паре стратегий (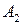 ,
, 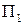 ) соответствует число
) соответствует число 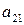 = –7, так как придется хранить 1 единицу сырья, что вызовет затраты 7 ден. ед. и т.д.
= –7, так как придется хранить 1 единицу сырья, что вызовет затраты 7 ден. ед. и т.д.
Таким образом, рассматриваемую ситуацию можно описать при помощи платежной матрицы:
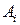
| 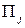
|
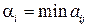
| ||
П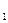 (20) (20)
| П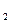 (21) (21)
| П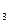 (22) (22)
| ||
А 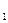 (20) (20)
| –10 | –20 | –20 | |
А 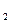 (21) (21)
| –7 | –10 | –10 | |
А 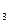 (22) (22)
| –14 | –7 | –0 | –14 |
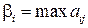
| -10 |
Данная игра не имеет решения в чистых стратегиях, так как 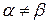 .
.
 2014-02-09
2014-02-09 954
954








