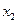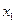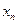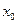Уравнение этого звена:
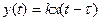
Выходной сигнал отстает по времени от изменения входного сигнала на величину транспортного запаздывания 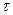 .
.
Используя теорему запаздывания преобразования Лапласа, получаем:
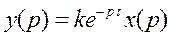 , отсюда
, отсюда
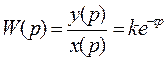
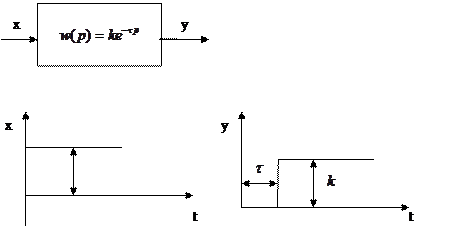

Если 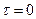 , то это - обычное усилительное звено.
, то это - обычное усилительное звено.
Частотная характеристика
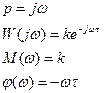


Способы соединения типовых элементарных звеньев (ТЭЗ)
1. Последовательное соединение
|
|
|
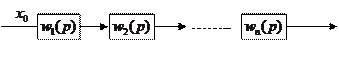

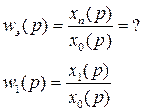
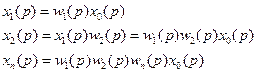
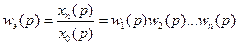
Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.
Пример.
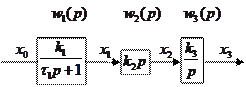

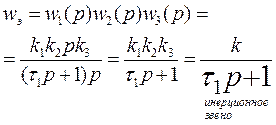
2. Параллельное соединение.
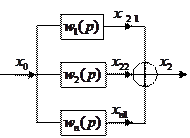

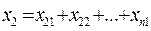
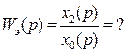
+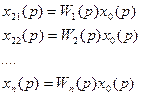
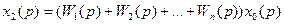
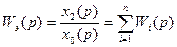

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев.
Пример.
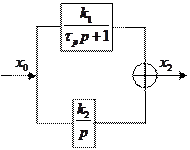

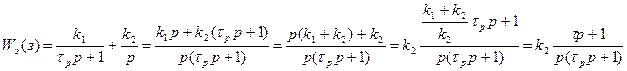
В результате параллельного соединения инерционного и интегрирующего звеньев получили дифференцирующее звено, интегрирующее и инерционное звенья. Т.о. не осуществляя операции дифференцирования с помощью дифференцирующей цепочки (эта операция плоха тем, что при дифференцировании вместе с полезным сигналом дифференцируются и помехи) получили эффект дифференцирования.
3. Соединение обратной связью
Это такое соединение когда часть выходного сигнала через элемент обратной связи подается на вход системы.
|
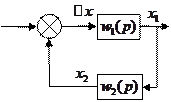

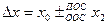
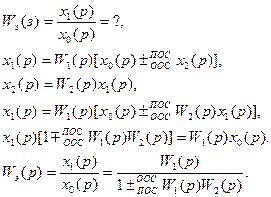
Передаточная функция звена, охваченного обратной связью, равна дроби, в числителе которой состоит передаточная функция прямой цепи, а в знаменателе 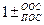 произведение передаточной функции прямой и обратной цепей.
произведение передаточной функции прямой и обратной цепей.
Пример:
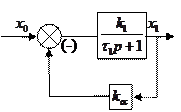

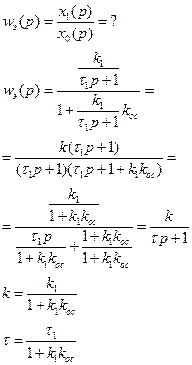
Инерционное звено охвачено жесткой отрицательной обратной связью. В результате получается тоже инерционное звено, меняются только параметры. Коэффициент усиления и постоянная времени уменьшаются в (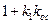 )раз.
)раз.
Получение передаточной функции замкнутой системы по управляющему и возмущающему воздействиям.
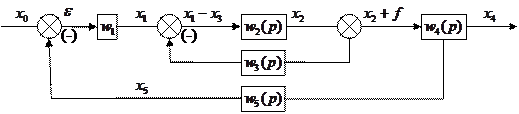

Мы рассмотрим линейные системы, к которым применим принцип суперпозиции. Это значит, что реакция системы на сумму воздействий, равна сумме реакций системы на каждое воздействие.
Поэтому при получении передаточной функции по управляющему воздействию положим 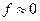 , а по возмущающему воздействию -
, а по возмущающему воздействию -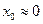
Получение передаточной функции по управляющему воздействию
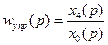
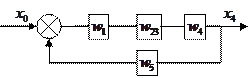

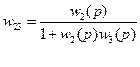
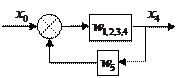

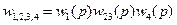
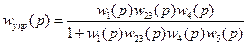
Получение передаточной функции по возмущающему воздействию.
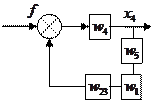

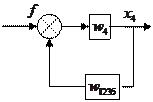

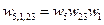
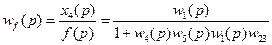
Обратите внимание: если выход один и тот же, то знаменатели передаточных функций по управляющему и по возмущающему воздействиям
(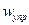 и
и 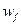 ) одинаковы.
) одинаковы.
Общее правило записи передаточной функции замкнутой системы по любому из приложенных воздействий.
Передаточная функция замкнутая по любому из приложенных воздей-
ствию равна дроби, в числителе которой стоит передаточная функция цепочки от места приложения воздействия до выхода, а в знаменателе
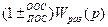 , где
, где 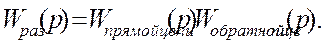
В домашней работе передаточные функции по управляющему и возмущающему воздействиям привести к виду:
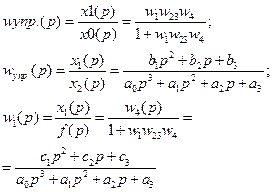
 2014-02-09
2014-02-09 661
661