Если на вход разомкнутой системы подать гармонический сигнал 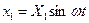 , где
, где 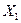 − амплитуда, а
− амплитуда, а 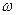 − угловая частота этого сигнала, то после окончания переходного процесса на выходе будет тоже гармоническая функция той же частоты, но иной амплитуды и сдвинутой по фазе относительно входной величины на угол
− угловая частота этого сигнала, то после окончания переходного процесса на выходе будет тоже гармоническая функция той же частоты, но иной амплитуды и сдвинутой по фазе относительно входной величины на угол 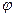 . Таким образом, для выходной величины можно записать:
. Таким образом, для выходной величины можно записать:
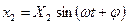 .
.
Итак, при прохождении гармонического сигнала через линейную систему возникают амплитудные и фазовые искажения сигнала, которые можно определить при помощи частотных характеристик.
Для построения частотных характеристик нужно в передаточной функции звена или системы заменить 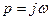 . В результате получим комплексную частотную функцию
. В результате получим комплексную частотную функцию 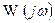 , модуль которой дает отношение амплитуд выходного сигнала к входному для любой частоты входного воздействия, а аргумент – фазовый сдвиг выходного сигнала по отношению к входному сигналу. Комплексная частотная функция
, модуль которой дает отношение амплитуд выходного сигнала к входному для любой частоты входного воздействия, а аргумент – фазовый сдвиг выходного сигнала по отношению к входному сигналу. Комплексная частотная функция 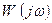 получила название амплитудно–фазовой частотной характеристики (а.ф.х.), которую можно представить в виде:
получила название амплитудно–фазовой частотной характеристики (а.ф.х.), которую можно представить в виде:
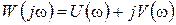
или в показательной форме
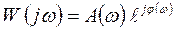 ,
,
где 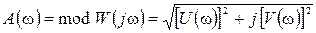 .
.
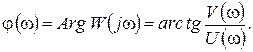
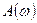 называется амплитудной частотной характеристикой (а.ч.х.), а
называется амплитудной частотной характеристикой (а.ч.х.), а 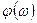 называется фазовой частотной характеристикой (ф.ч.х.). Характеристику
называется фазовой частотной характеристикой (ф.ч.х.). Характеристику 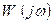 можно построить в прямоугольных координатах по выражениям
можно построить в прямоугольных координатах по выражениям 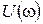 и
и 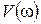 при изменении частоты входного сигнала
при изменении частоты входного сигнала 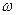 от
от 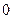 до
до 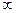 (рис. 3.1). Ее можно также построить в полярных координатах на комплексной плоскости по выражениям
(рис. 3.1). Ее можно также построить в полярных координатах на комплексной плоскости по выражениям 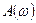 и
и 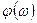 при изменении частоты
при изменении частоты 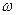 от
от 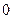 до
до 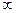 (рис. 3.2).
(рис. 3.2).
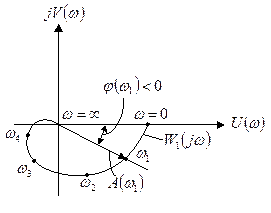
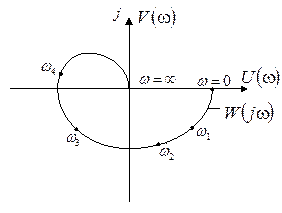
Рис. 3.1 Рис. 3.2
Данные кривые строятся по точкам на комплексной плоскости по вычисленным значениям 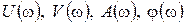 при изменении частоты от
при изменении частоты от 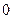 до
до 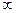 .
.
 2014-02-09
2014-02-09 502
502








