Данный критерий является алгебраическим и позволяет судить об устойчивости
замкнутой системы по коэффициентам характеристического уравнения замкнутой системы:
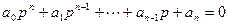 .
.
Для этого уравнения составим квадратную матрицу коэффициентов, содержащую 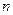 строк и
строк и 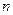 столбцов:
столбцов:
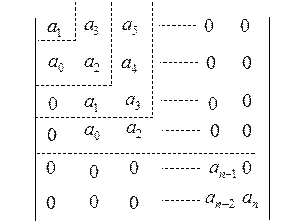 |

Эта таблица составляется следующим образом.
В верхней строке пишутся все коэффициенты характеристического уравнения с нечетными индексами, во второй – с четными, начиная с 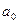 . После них пишется несколько нулей так, чтобы в строках было
. После них пишется несколько нулей так, чтобы в строках было 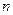 элементов. Третья и четвертая строки – это первые две строки, сдвинутые на один элемент вправо и т.д. Всего должно быть
элементов. Третья и четвертая строки – это первые две строки, сдвинутые на один элемент вправо и т.д. Всего должно быть 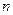 столбцов.
столбцов.
Для устойчивости линейной системы необходимо и достаточно, чтобы были положительны 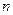 определителей Гурвица, которые имеют вид:
определителей Гурвица, которые имеют вид:
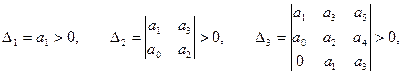 и т.д.
и т.д.
Последний определитель Гурвица определяется следующим образом:
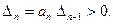
Граница устойчивости определяется из условия 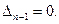
Например, найдем условия устойчивости для системы третьего порядка:
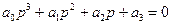 .
.
Составим матрицу коэффициентов
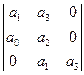
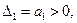
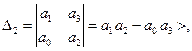 при
при 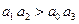 .
.
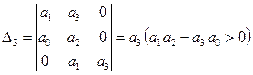 , при
, при 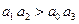 .
.
Для устойчивости линейной системы третьего порядка недостаточно положительности коэффициентов характеристического уравнения, а дополнительно требуется выполнение условия 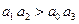 .
.
 2014-02-09
2014-02-09 581
581








