Частотный критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду а.ф.х. разомкнутой системы.
Передаточная функция разомкнутой системы имеет вид:
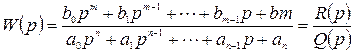 .
.
При доказательстве критерия сделаем следующие допущения:
1. Разомкнутая система устойчива.
2. 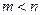 .
.
Введем вспомогательную функцию:
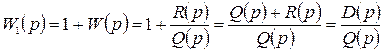 ,
,
где 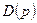 − характеристический многочлен замкнутой системы, а
− характеристический многочлен замкнутой системы, а  − характеристический многочлен разомкнутой системы.
− характеристический многочлен разомкнутой системы.
Заменяя 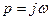 , получим:
, получим:
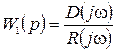 .
.
По критерию Михайлова угол поворота вектора 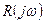 при
при 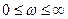 равен
равен  , т.к. разомкнутая система устойчива по условию. С другой стороны, требуется, чтобы система была устойчивой в замкнутом состоянии. Для этого нужно потребовать, чтобы угол поворота вектора
, т.к. разомкнутая система устойчива по условию. С другой стороны, требуется, чтобы система была устойчивой в замкнутом состоянии. Для этого нужно потребовать, чтобы угол поворота вектора 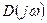 при
при 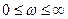 также равнялся бы
также равнялся бы  .
.
Отсюда следует, что угол поворота вектора 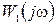 должен быть равен:
должен быть равен:
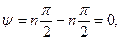 т.к. при делении комплексных чисел аргументы вычитаются.
т.к. при делении комплексных чисел аргументы вычитаются.
Частотная характеристика  представлена на рис. 4.3.
представлена на рис. 4.3.
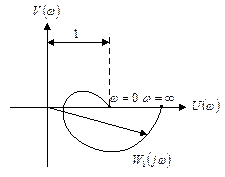
Рис. 4.3.
Условие  означает, что частотная функция
означает, что частотная функция  не должна охватывать начало координат. Вернемся теперь к функции:
не должна охватывать начало координат. Вернемся теперь к функции:
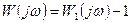 ,
,
которая представляет собой амплитудно-фазовую частотную характеристику разомкнутой системы (рис. 4.4).
Отсюда получаем следующую формулировку частотного критерия Найквиста.
Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку 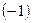 .
.
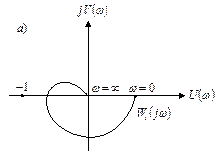 | |||||
 | |||||
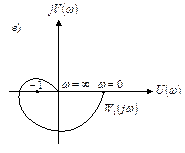 | |||||
Рис. 4.4
Случаи, когда система нейтральна в разомкнутом состоянии, и неустойчивой разомкнутой системы, рассмотрены в [1].
 2014-02-09
2014-02-09 447
447








