Определение устойчивости по логарифмическим
Для определения устойчивости по критерию Нейквиста можно строить не амплитудно-фазовую характеристику, а логарифмическую амплитудную частот-ную характеристику (л.а.х) и логарифмическую фазовую частотную характеристику (л.ф.х) разомкнутой системы.
Построение л.а.х. производится по выражению:
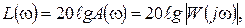
где 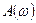 - модуль частотной передаточной функции разомкнутой системы.
- модуль частотной передаточной функции разомкнутой системы.
Построение л.ф.х. производится по выражению 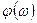 частотной передаточной функции.
частотной передаточной функции.
Наиболее простое построение получается, если передаточную функцию разомкнутой системы можно свести к виду
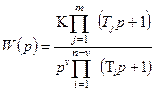 .
.
После подстановки 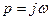 получаем:
получаем:
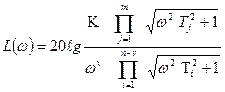 .
.
Логарифмическая фазовая частотная характеристика определяется выражением:
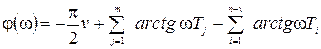 .
.
Логарифмическую амплитудно-частотную характеристику можно строить непосредственно по заданной передаточной функции. Для этого надо помнить, что, согласно характеристикам типовых звеньев, каждому сомножителю типа 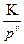 соответствуют л.а.х. с наклоном
соответствуют л.а.х. с наклоном 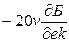 , имеющие при
, имеющие при 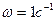 ординату, равную
ординату, равную
-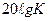 . Каждому сомножителю типа
. Каждому сомножителю типа 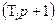 в знаменателе соответствует точка излома характеристики при
в знаменателе соответствует точка излома характеристики при 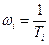 с последующим наклоном
с последующим наклоном 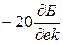 , а каждому сомножителю такого же типа в числителе соответствует точка излома при
, а каждому сомножителю такого же типа в числителе соответствует точка излома при 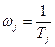 с последующим наклоном
с последующим наклоном 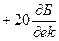 . Сомножителю же типа
. Сомножителю же типа 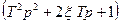 в знаменателе соответствует излом при
в знаменателе соответствует излом при 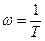 с наклоном
с наклоном 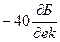 , если
, если 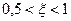 .
.
Пример.
Построим л.а.х. разомкнутой системы с передаточной функцией в разомкнутом состоянии:
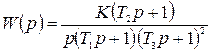 .
.
Примем, что выполняется условие 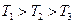 . Тогда для сопрягающих частот будет выполнятся условие
. Тогда для сопрягающих частот будет выполнятся условие 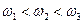 . Если
. Если 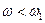 , то можно пренебречь всеми постоянными времени и передаточная функция будет равна:
, то можно пренебречь всеми постоянными времени и передаточная функция будет равна:
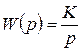 .
.
Поэтому из точки, где 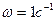 , восстанавливаем перпендикуляр, равный
, восстанавливаем перпендикуляр, равный 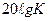 , и через эту точку проводим низкочастотную асимптоту с наклоном
, и через эту точку проводим низкочастотную асимптоту с наклоном 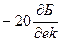 , которую продолжаем до первой сопрягающей частоты. Если эта сопрягающая частота соответствует постоянной времени в знаменателе, то л.а.х. «изламываем» вниз на
, которую продолжаем до первой сопрягающей частоты. Если эта сопрягающая частота соответствует постоянной времени в знаменателе, то л.а.х. «изламываем» вниз на 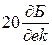 и проводим до следующей сопрягающей частоты. Если эта сопрягающая частота соответствует постоянной времени, находящейся в числителе, то л.а.х. «изламывается» вверх на
и проводим до следующей сопрягающей частоты. Если эта сопрягающая частота соответствует постоянной времени, находящейся в числителе, то л.а.х. «изламывается» вверх на 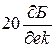 и проводится до следующей сопрягающей частоты и т.д.
и проводится до следующей сопрягающей частоты и т.д.
Построенная по данному правилу л.а.х. представлена на рис. 4.5.
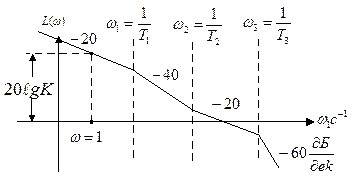
Рис. 4.5
Выражение для фазовой частотной характеристики принимает вид:
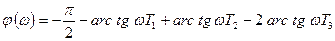 .
.
Рассмотрим теперь определение устойчивости по построенным л.а.х. и л.ф.х. Ограничимся случаем, когда разомкнутая система устойчива. Другие случаи см. [1].
Пусть а.ф.х. разомкнутой системы имеет вид, представленный на рис. 4.6 а. Система находится на границе устойчивости. В этом случае 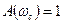 или
или 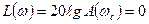 при
при 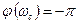 . Поэтому такому начертанию а.ф.х. будет соответствовать следующее расположение л.а.х. и л.ф.х. (рис. 4.6, б,в).
. Поэтому такому начертанию а.ф.х. будет соответствовать следующее расположение л.а.х. и л.ф.х. (рис. 4.6, б,в).
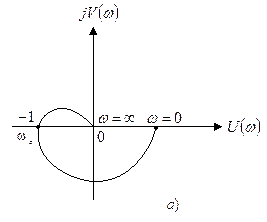
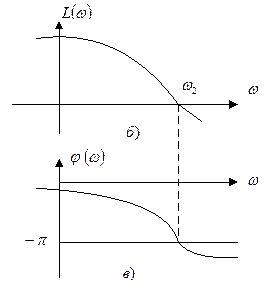
Рис. 4.6
Пусть а.ф.х. разомкнутой системы имеет вид (рис. 4.7).
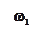
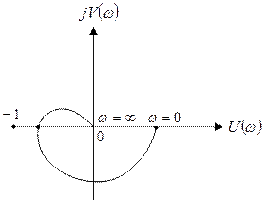
Рис. 4.7
Согласно критерию устойчивости Найквиста, замкнутая система будет устойчива. В этом случае 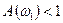 или
или 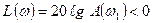 при
при 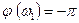 .
.
Поэтому такому начертанию а.ф.х. будет соответствовать следующее расположение л.а.х. и л.ф.х. (рис. 4.8).
Аналогично для неустойчивой системы 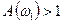 или
или 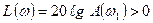 при
при 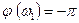 (рис. 4.9).
(рис. 4.9).
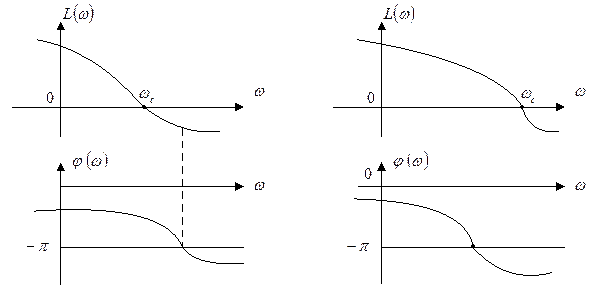 |
Рис. 4.8 Рис. 4.9
Отсюда следует, что для устойчивости замкнутой системы, для всех частот, при которых ординаты л.а.х. положительны, л.ф.х. не должна пересекать линию 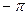 .
.
 2014-02-09
2014-02-09 463
463








