Необходимое и достаточное условие устойчивости

Устойчивость линейных систем

Понятие устойчивости связано со способностью системы возвращаться в состояние равновесия после исчезновения сил, которые вывели его из этого равновесия. Это означает, что переходный процесс должен затухать. Устойчивость является необходимым, но недостаточным условием работоспособности системы, т.к. при этом неизвестно быстродействие системы, точность в установившемся режиме, число колебаний и т.д.

В общем случае динамика линейной САУ описывается дифференциальным уравнением вида:

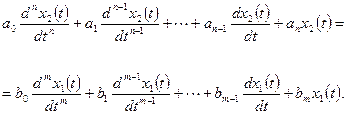(4.1)

Как известно из теории дифференциальных уравнений, решение уравнения (4.1) находится как сумма двух решений:

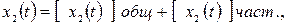
где 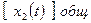− общее решение однородного дифференциального уравнения, т.е. решение уравнения (4.1) без правой части, которое представляет собой переходную составляющую, т.е. свободное движение системы;

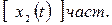− это частное решение уравнения (4.1.), т.е. решение уравнения (4.1.) с правой частью, которое представляет собой установившийся процесс и называется вынужденным движением.

Поэтому .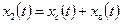

Система будет устойчивой, если при 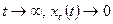. Общее решение (при отсутствии кратных корней) ищется в виде:

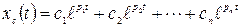, (4.2)

где 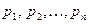− корни характеристического уравнения, 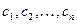− постоянные интегрирования, определяемые из начальных условий.

Корни характеристического уравнения могут быть вещественными, комплекс-ными и чисто мнимыми.

Рассмотрим эти случаи.

Вещественный корень. Пусть один из корней, например 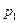, является вещественным. Если он отрицательный 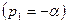, то слагаемое, определяемое этим корнем в (4.2), будет представлять собой экспоненту 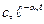. Очевидно, что при 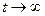этот член будет затухать.

При 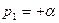получится не затухающий, а расходящийся процесс.

Комплексные корни. При отрицательной вещественной части два корня, например 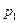и 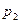, будут иметь вид . В этом случае слагаемые, определяемые этими корнями в уравнении (4.2), могут быть представлены в виде:

,

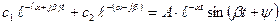где 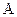и 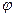− новые постоянные интегрирования.

Нетрудно видеть, что в этом случае получаются затухающие колебания.

При положительной вещественной части колебания будут не затухающими, а расходящимися.

Чисто мнимые корни. В этом случае 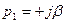и 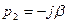. Слагаемое, определяемое этими корнями в уравнении (4.2), будет представлять собой незатухающие колебания, т.е. колебания с постоянной амплитудой:

.

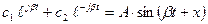Следовательно, для затухания переходного процесса необходимо, чтобы вещественные части всех корней характеристического уравнения были отрицательными.

При наличии чисто мнимых корней в системе возникают незатухающие гармонические колебания, что соответствует границе устойчивости.

Характеристическое уравнение замкнутой системы можно найти из уравнения (4.1), если в нем приравнять правую часть нулю и обозначить .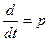

Тогда

,

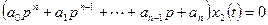откуда характеристическое уравнение примет вид:

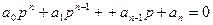(4.3)

Далеко не всегда бывает легко вычислить корни характеристического уравнения. Поэтому желательно иметь такие критерии, с помощью которых можно было бы судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения, без вычисления корней. Эти критерии называются критериями устойчивости.

В устойчивой системе вещественные части всех корней характеристического уравнения должны быть отрицательными, поэтому все коэффициенты характеристического уравнения должны быть положительными [1].

Таким образом, положительность коэффициентов характеристического уравнения является необходимым, но не достаточным условием устойчивости.