Основные понятия. Множество – совокупность элементов, обладающих каким-то одним общим свойством

Множество – совокупность элементов, обладающих каким-то одним общим свойством.

Множество обозначают: M,N …..

m₁, m₂,.., m_n – элементы множества.

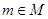– принадлежность элемента m к множеству M.

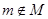
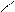– непринадлежность элемента m к множеству M.

Пример 1. Числовые множества:

· 1,2,3,… множество натуральных чисел N;

· 0,1,2,3,… множество натуральных чисел, включая 0 N₀;

· …,-2,-1,0,1,2,… - множество целых чисел Z;

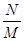· множество рациональных чисел.

Пустое множество - множество, не содержащее элементов. Обозначается символом Æ.

Пример 2. Пустое множество: сумма углов D ¹ 180⁰ пустое: M = Æ.

Множество А называется подмножеством В, если всякий элемент a является элементом b.

А Í В – А подмножество В (нестрогое включение), Í - знак нестрогого включения.

Если А Í В и А ¹ В то А Ì В (строгое включение).

Если А Í В, то множество А называется подмножеством множества В (также говорят, что В покрывает А). Если при этом А ¹ В, то множество А называется собственным подмножеством А Ì В ( рис. 1.1).

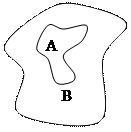
Рис. 1.1. Строгое включение множества А в В АÌВ.

Два определения равенства множеств:

1) Множества А и В равны, если их элементы совпадают A = B;

2) Множества А и В равны, если aeyrwbz

3).

Пусть A — множество. Множество всех подмножеств множества A называется булеаном A (также степенью множества, показательным множеством или множеством частей) и обозначается Р(А) или 2^A. Ясно, что 0ÎР(А) и АÎР(А).

Утверждение. Число подмножеств конечного множества, состоящего из n элементов равно 2 ⁿ.

Доказательство. Если n = 0, т.е. множество пусто, то у него только одно подмножество – оно само, и интересующее нас число равно 2⁰ = 1.

Пусть утверждение справедливо для некоторого n и пусть M – множество с кардинальным числом n + 1. Зафиксировав некоторый элемент а₀ÎМ, разделим подмножества множества M на два типа:

1. содержащие a ₀,

2. не содержащие a ₀, то есть являющиеся подмножествами множества М – {а₀}.

Подмножеств типа (2) по предположению 2 ⁿ. Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента a ₀ и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1). Поэтому число всех подмножеств множества M равно 2ⁿ + 2ⁿ = 2^{n + 1}.

Множества бывают конечные и бесконечные.

Конечное множество имеет конечное количество элементов, в противном случае множество называется бесконечным.

Мощность множества - число элементов конечного множества. Обозначается как |М|.

Если дано множество Е и мы рассматриваем все его подмножества, то множество Е называется универсальным множеством.

Пример 3. Если за Е взять множество книг, то его подмножества: книги по математике, биологии, физике, химии…

Если универсальное множество состоит из n элементов, то число подмножеств = 2ⁿ.

Если 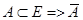, состоящее из элементов E, не принадлежащих А, называется дополненным.

Три способа задания множества:

1) Перечислением, то есть списком своих элементов. Списком можно задать лишь конечные множества. Обозначение списка – в фигурных скобках. Например, множество А специальности университета А={менеджмент организации, управление персоналом, автоматизация производства};

2) Описанием характеристических свойств, которыми должны обладать его элементы. Например, А все целые числа в интервале 1<x<5. А={2, 3, 4};

3) Порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов, либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры. Например, А множество корней уравнения х² − 3 х + 2 = 0. А={1, 2}.