Вектором ( кортежем) в линейной алгебре и дискретной математике называют упорядоченный набор элементов.
Элементы, определяющие вектор, называются координатами или компонентами. Координаты нумеруются слева направо, а их число называется длиной или размерностью вектора. В отличие от элементов множества, координаты вектора могут совпадать. Координаты вектора заключаются в круглые скобки, например 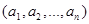 . Иногда скобки или запятые опускаются.
. Иногда скобки или запятые опускаются.
Два вектора равны, если они имеют равную длину и их соответствующие координаты равны. Иначе говоря, векторы 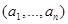 и
и  равны, если
равны, если 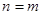 и
и 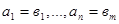 .
.
Прямым произведением множеств А и В (обозначение 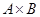 ) называется множество всех упорядоченных пар
) называется множество всех упорядоченных пар 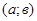 , таких, что
, таких, что 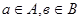 . В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А2. Аналогично, прямым произведением множеств
. В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А2. Аналогично, прямым произведением множеств  называется множество всех векторов
называется множество всех векторов 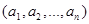 длины п, таких, что
длины п, таких, что 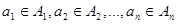 .
.
Пример 7 .
Множество 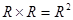 - это множество всех упорядоченных пар действительных чисел, геометрической интерпретацией которого служит декартова координатная плоскость. Координатное представление точек плоскости было впервые предложено Р. Декартом и исторически является первым примером прямого произведения. Поэтому часто прямое произведение множеств называют декартовым произведением.
- это множество всех упорядоченных пар действительных чисел, геометрической интерпретацией которого служит декартова координатная плоскость. Координатное представление точек плоскости было впервые предложено Р. Декартом и исторически является первым примером прямого произведения. Поэтому часто прямое произведение множеств называют декартовым произведением.
Пример 8 .
Даны множества 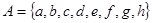 и
и 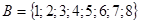 . Тогда
. Тогда 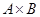 есть множество обозначений клеток шахматной доски.
есть множество обозначений клеток шахматной доски.
Проекцией вектора 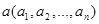 на некоторую ось называется его компонента (координата) с соответствующим порядковым номером (обозначается прia). Например, проекция точки плоскости на 1-ю ось есть её абсцисса (первая координата).
на некоторую ось называется его компонента (координата) с соответствующим порядковым номером (обозначается прia). Например, проекция точки плоскости на 1-ю ось есть её абсцисса (первая координата).
Теорема. Мощность произведения конечных множеств 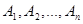 равна произведению мощностей этих множеств:
равна произведению мощностей этих множеств: 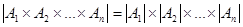 .
.
Следствие. 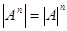 .
.
 2014-02-09
2014-02-09 869
869








