Лекция 2. Молекулярно-кинетическое описание свойств идеального газа

Модель идеального газа: учитываются лишь столкновения молекул газа со стенками. При этом давление определяется как сила ударов молекул, усредненная во времени и отнесенная к единице площади.

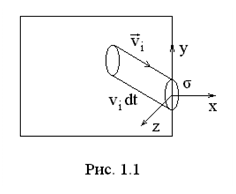Разделим молекулы на группы по значениям скорости. В 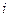– ой группе скорость всех молекул в данный момент времени равна 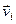. Молекулы, которые ударятся о площадку 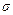на стенке сосуда за время 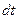находятся внутри наклонного цилиндра с основанием 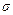и образующей 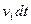(рис. 1.1). Число ударов таких молекул за время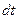

,

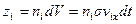где 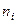- концентрация молекул в 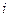- ой группе, 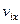- проекция скорости 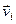на ось 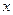, перпендикулярную площадке .

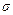При ударе каждая молекула газа сталкивается с молекулой стенки. При этом средняя энергия молекул газа не изменяется. Для удобства вычислений разделим процесс взаимо-действия со стенкой на два этапа: 1) “прилипание” к стенке (остановка); 2) отталкивание от стенки.

Первый этап. Полный импульс молекул 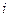- ой группы

.

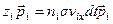Сила, действующая на площадку 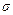со стороны молекул 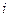- ой группы на этом этапе

.

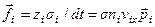Сила со стороны всех молекул газа

.

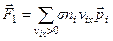Второй этап. Сила со стороны всех молекул на втором этапе (сила отдачи)

.

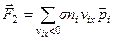Тогда полная сила, действующая на площадку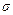

.

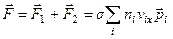Из хаотичности движения следует, что

, .

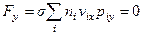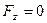При этом проекция силы на ось 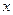всегда больше нуля

.

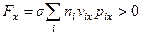Следовательно, давление газа

.

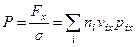Определим среднее от произведения 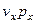по всем молекулам

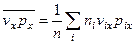, где 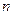- полная концентрация молекул.

Тогда давление идеального газа можно представить в виде

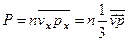, (1)

так как в силу хаотичности движения молекул .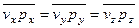

Уравнение (1) называется основным уравнением молекулярно-кинетической теории идеального газа. В такой форме оно применимо и к релятивистским частицам. В частности, с помощью него можно вычислить давление фотонного газа. Для молекул, движущихся по законам классической механики 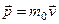и уравнение (1) принимает вид

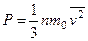. (2)

Введем понятие среднеквадратичной скорости молекул 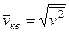. Умножая (2) на молярный объем газа 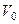, получим

, .

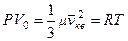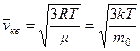Тогда для средней кинетической энергии молекул 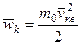получим

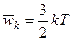. (3)

Выражение (3) справедливо только для одноатомных молекул, так как мы считали молекулы материальными точками. Оно позволяет определить абсолютную температуру как меру средней кинетической энергии теплового движения молекул.

В курсе механики мы определили число степеней свободы тела 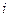как наименьшее число координат, необходимых для определения положения тела в пространстве.

Одноатомная молекула: .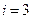

Двухатомная молекула: 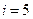(три координаты центра масс и два угла относительно двух взаимно перпендикулярных осей, проходящих через центр масс).