Основные понятия. Всякая поверхность в пространстве задается в декартовых координатах уравнением вида

Всякая поверхность в пространстве задается в декартовых координатах уравнением вида .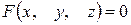

Если 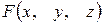‑ многочлен 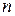-й степени, то соответствующая поверхность называется алгебраической поверхностью 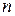-го порядка или просто поверхностью 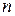-го порядка.

Всякая поверхность 1-го порядка есть плоскость, т.е. всякое уравнение 1-й степени

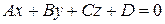
(1)

определяет плоскость. Уравнение (1) называется общим уравнением плоскости.

Вектор 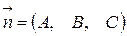, координатами которого являются коэффициенты при 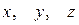в уравнении (1) перпендикулярен плоскости (1) по свойству 4 скалярного произведения векторов. Этот факт будет постоянно использоваться в дальнейшем. Вектор 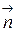называют нормальным вектором плоскости (1).

Уравнение плоскости, проходящей через данную точку 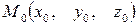перпендикулярно вектору 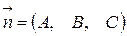, имеет вид

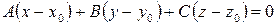
(2)

Очевидно, что уравнение (1) имеет смысл только тогда, когда хотя бы один из коэффициентов 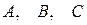не равен нулю.

Рассмотрим частные случаи.

I.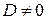

1. если 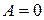, то уравнение 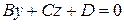определяет плоскость, параллельную оси 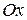, так как вектор нормали к этой плоскости 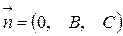перпендикулярен оси 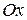(проекция ненулевого вектора на ось равна нулю тогда, когда он перпендикулярен этой оси).

2. Аналогично, если 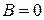, то уравнение 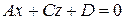определяет плоскость, параллельную оси .

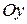3. Если 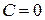. То уравнение 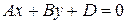определяет плоскость, параллельную оси .

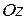4. Если 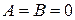, то уравнение 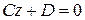или 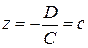определяет плоскость, параллельную плоскости 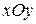. В этом случае вектор нормали 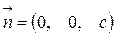перпендикулярен к осям 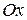и 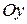, т.е. к плоскости .

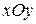5. При 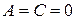имеем 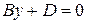или 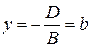‑ уравнение плоскости, параллельной координатной плоскости .

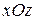6. Если 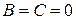, то уравнение 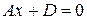или 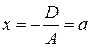определяет плоскость, параллельную плоскости .

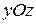II. .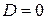

1. Если 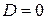, то уравнение 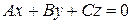определяет плоскость, проходящую через начало координат, так как координаты точки 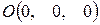удовлетворяют этому уравнению.

2. Если 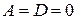, то уравнение 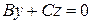определяет плоскость, вектор нормали которой 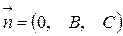. Эта плоскость проходит через ось .

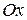3. Аналогично, если 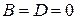, то уравнение 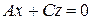определяет плоскость, проходящую через ось .

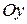4. Если 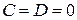, то уравнение 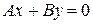определяет плоскость, проходящую через ось .

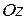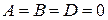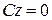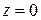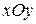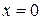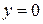5. Если , то уравнение или определяет плоскость . Аналогично, уравнения и определяют соответственно плоскост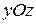и и .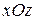

Если в уравнении (1) все коэффициенты 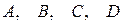отличны от нуля, то это уравнение может быть преобразовано к уравнению плоскости в отрезках:

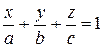
(3)

Здесь 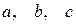‑ величины отрезков, отсекаемых плоскостью на осях координат (Рис. 8.1).