Смешанным произведением тройки векторов 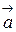 ,
,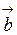 и
и 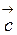 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 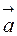 на векторное произведение
на векторное произведение 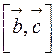 . Если рассматриваемые векторы
. Если рассматриваемые векторы 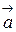 ,
,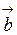 и
и 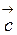 некомпланарны, то векторное произведение
некомпланарны, то векторное произведение 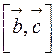 есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор
есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор 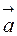 , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов
, то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов 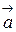 ,
,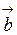 и
и 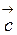 , и его высоты, т.е. объему этого параллелепипеда.
, и его высоты, т.е. объему этого параллелепипеда.
Таким образом, смешанное произведение векторов 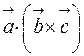 (которое обозначается
(которое обозначается 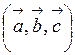 ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах 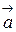 ,
,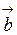 и
и 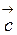 .
.
Знак произведение положителен, если векторы 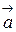 ,
,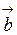 и
и 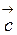 , образуют правую тройку векторов, т.е. вектор
, образуют правую тройку векторов, т.е. вектор 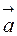 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 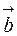 к
к 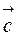 виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки.
Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов 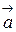 ,
,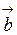 и
и 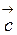 : для того, чтобы векторы
: для того, чтобы векторы 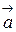 ,
,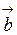 и
и 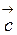 были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.
были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.
Если 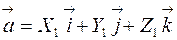
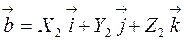 , и
, и 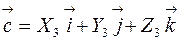 то
то 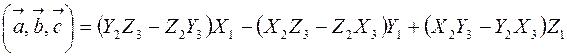 ,
,
или в свернутой форме
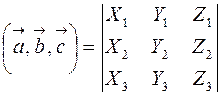 .
.
Справедливы следующие свойства смешанного произведения векторов:
1. Смешанное произведение не меняется при циклической перестановке его сомножителей 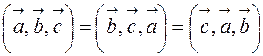 ;
;
2. При перестановке двух соседних множителей смешанное произведение меняет свой знак на противоположный 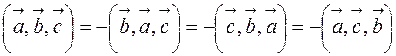 .
.
 2014-02-09
2014-02-09 614
614








