2014-02-09
851
Контрольные вопросы к теме
1. Понятие поверхности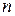 
-го порядка.
2. Общее уравнение плоскости.
3. Понятие нормального вектора плоскости.
4. Уравнение плоскости в отрезках.
5. Нормальное уравнение плоскости.
6. Вычисление отклонения точки от плоскости.
Основные понятия, включенные в систему тренинг-тестирования:
эллипс; гипербола; парабола; фокусы эллипса; уравнение эллипса; каноническое уравнение эллипса; эксцентриситет эллипса; фокальные радиусы; директрисы эллипса; фокусы гиперболы; каноническое уравнение гиперболы; асимптота гиперболы; оси гиперболы; вершины гиперболы; полуоси гиперболы; эксцентриситет гиперболы; фокальные радиусы гиперболы; директрисы гиперболы; каноническое уравнение параболы; ось параболы.
Уравнение фигуры.
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестным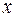и 
и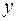 
записывается в виде 
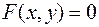. Если выбрать на плоскости некоторую прямоугольную систему координат, то в ней уравнение называется уравнением фигуры 
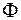при выполнении следующих двух условий:
- Если точка
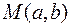принадлежит фигуре 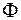, то координаты 
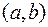являются решениями уравнения 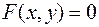, т.е. 
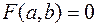; - если пара чисел
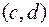является решением уравнения 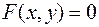, то точка 
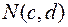принадлежит фигуре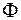
Это определение в более компактной записи выглядит следующим образом. Уравнение 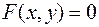называется уравнением фигуры, если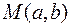 
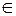
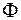
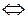
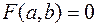, то есть 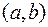– решение уравнения .
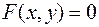Из определения уравнения фигуры следует, что фигура 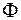состоит только из тех точек плоскости, координаты которых являются решениями уравнения 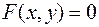, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение 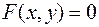и надо построить фигуру 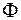, уравнением которой является ;
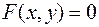- дана фигура 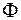и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 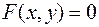и решается чаще всего методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
