Азимутальные проекции

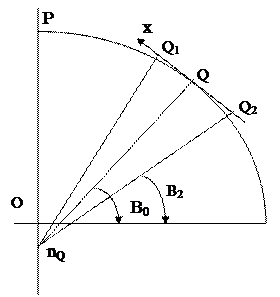
Французский инженер Руссиль в 1924 году предложил для геодезических и топографических работ проекцию на касательную плоскость, являющуюся частным случаем азимутальных проекций, характеристическое уравнение которой можно получить следующим образом (см. рис. 7. 5)

Рис. 7. 5

Здесь за длину дуги осевого меридиана PQ, заключенного между точками Q1 и Q2 принимается дуга окружности радиусом, равным среднему радиусу кривизны эллипсоида в точке Q с широтой В0, который имеет известное нам выражение через главные радиусы кривизны эллипсоида 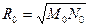. Из рисунка получаем связь между длиной дуги окружности и ее касательной. Длина дуги окружности, заключенной между симметрично расположенными, относительно центральной, точками Q1 и Q2 (для изображаемой области) выражается уравнением

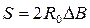
Здесь DВ = В – В₀, а длина изображения осевого меридиана на плоскости проекции (касательной к окружности в точке Q)

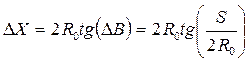
Разлагая в ряд функцию малого аргумента, получаем

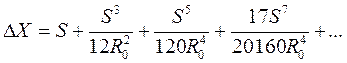(7. 44)

В общем случае, когда картинная плоскость может не только касаться поверхности эллипсоида, но и пересекать ее (секущая плоскость), можем записать уравнение (7. 44) для азимутальных проекций в виде

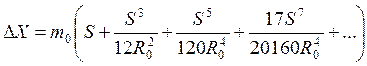. (7. 45)

Учитывая то, что в проекции Гаусса – Крюгера осевой меридиан изображается на плоскости без искажений, в данном уравнении под S можем понимать значение, полученное по формуле для этой проекции, а в (7. 35) положить m₀ = 1. После тождественных преобразований получаем для коэффициентов характеристического уравнения азимутальных проекций

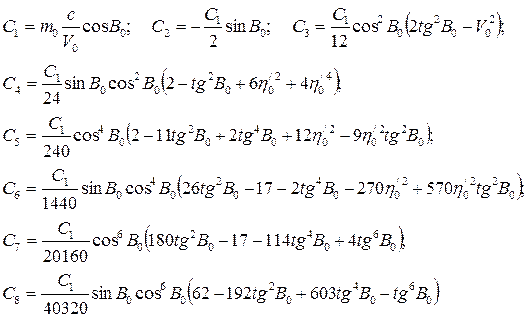(7. 46)

В азимутальных проекциях также имеется возможность управления распределением искажений внутри изображаемой области, моделируя значение m₀ £ 1. При этом, полагая m₀ = 1, получим проекцию Руссиля.

Азимутальные проекции удобно применять для областей округлой формы.