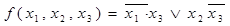
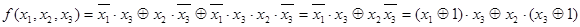 =
=
=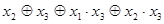
Двоичные функции можно также задавать многочленами, в которых используются операции сложения, вычитания и умножения действительных чисел. Так, непосредственно проверкой убеждаемся, что
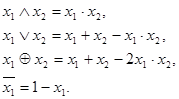
Поскольку каждую двоичную функцию можно задать своим многочленом Жегалкина, СДНФ или СКНФ, то,заменив все используемые в этих формулах операции на их выражения (по приведенным выше формулам) и раскрыв затем скобки получаем для всякой двоичной функции эквивалентную запись в виде некоторого действительного многочлена. Вместе с тем, можно заметить, что такая запись неоднозначна. Например, функцию 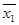 можно представить действительными многочленами вида:
можно представить действительными многочленами вида:
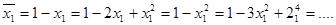
Перечисленные многочлены при 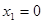 и
и 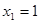 принимают значения 1 и 0 соответственно. Все многочлены в этом примере обладают той особенностью, что они содержат степени переменной
принимают значения 1 и 0 соответственно. Все многочлены в этом примере обладают той особенностью, что они содержат степени переменной  , в то же время для двоичных переменных очевидны равенства:
, в то же время для двоичных переменных очевидны равенства:
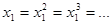
Если отказаться от использования переменных в степенях выше первой, то неоднозначность представления двоичных функций можно исключить.
Теорема 2.2.4. Любая двоичная функция 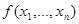 однозначно представляется в виде следующего действительного многочлена:
однозначно представляется в виде следующего действительного многочлена:
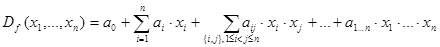
все коэффициенты,которого являются целыми числами.
Доказательство. Полностью аналогично тому, которое было приведено в теореме 2.2.2. Необходимо только заменить операцию «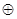 » на «+».
» на «+».
Ниже, говоря «действительный многочлен», будем всюду иметь в виду определенный в теореме 2.2.4 многочлен 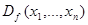
 2014-02-09
2014-02-09 698
698








