Псевдобулевы функции

Лекция №4.

Пусть Р- произвольное поле. Элементы 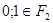будем рассматривать как нуль и единицу поля .

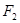Определение 4.1.1. Псевдобулевой функцией от 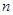переменных, или 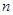-местной псевдобулевой функцией, над полем Р при 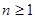называется любое отображение 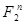в Р. Нуль-местными псевдобулевыми функциями над Р называются все элементы поля Р.

Множество всех пседобулевых функций от 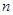переменных над полем Р обозначим через 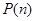. В частности, при 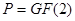класс 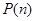совпадает с классом булевых функций 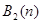. В других случаях эти классы различны и если условиться, псевдобулеву функцию со значением из 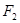считать булевой, то: .

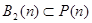Множество функций 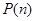относительно естественным образом определяемых операций сложения функций и умножения функций на элементы из Р образуют линейное пространство над полем Р.

Рассмотрим систему функций:

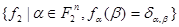(4.1.2)

,где 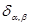-символ Кронекера, т.е.: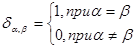

Утверждение 4.1.3. Система функций (4.1.2) является базисом пространства .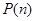

Доказательство. Очевидно, что система (4.1.2) – линейно независимая система. Далее пусть 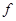- произвольная функция из 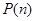. Тогда очевидно, что:

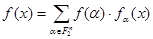(4.1.4)

Отсюда следует, что (4.1.2) – базис пространства .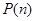

Замечание 4.1.5. Если 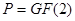, то 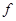- булева функция и разложение (4.1.4) функции 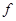совпадает с разложением, полученным заменой в её СДНФ операции 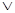на .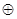

Замечание 4.1.6. Если 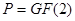, то система функций:

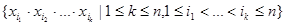(4.1.7)

является базисом пространства 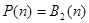. Это следует из теоремы 2.2.4 об однозначном представлении булевых функций многочленами Жегалкина. В этом случае представление функции многочленом Жегалкина есть (4.1.7).

Замечание 4.1.8. Представление булевых функций через базисы пространства 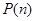сопряжено со многими трудностями. Вот две из них:

1. Непростым является вопрос об описании базисов пространства ;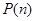

2. Если даже имеется система функций являющаяся базисом пространства, то в общем случае сложным является вопрос о нахождении коэффициентов в разложении булевой функции по указанному базису.

Замечание 4.1.9. В решении вопроса об описании базисов пространства 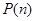иногда оказывается полезным переход от пространства 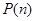к пространству 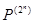векторов-столбцов длинны 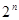над полем Р. Сопоставим каждой функции 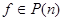вектор столбец значений 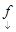этой функции. В итоге получаем отображение 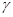пространства 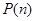в пространство 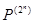. Нетрудно видеть, что 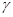есть изоморфизм пространств, а поэтому система функций 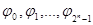является базисом пространства 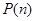тогда и только тогда, когда матрица 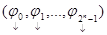является невырожденной.