Сопоставим каждому двоичному вектору 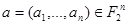 линейную двоичную функцию
линейную двоичную функцию 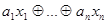 (сокращенно (
(сокращенно (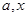 )), и определим функции:
)), и определим функции:
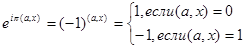
Например, векторам 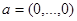 и
и 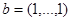 соответствуют из функции
соответствуют из функции
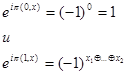
соответственно. Всего имеется 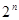 функций вида
функций вида 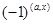 . Как показывает следующая лемма, они образуют ортогональную систему функций.
. Как показывает следующая лемма, они образуют ортогональную систему функций.
Лемма 2.3.1. Для любых векторов 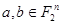 справедливы равенства
справедливы равенства 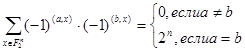
Доказательство. Сначала заметим, что 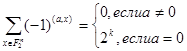
Поскольку линейная функция 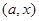 при
при 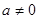 принимает значение 0 ровно
принимает значение 0 ровно 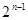 . Теперь
. Теперь
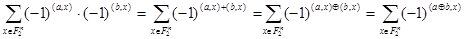 . Отсюда и следует утверждение леммы.
. Отсюда и следует утверждение леммы.
Теорема 2.3.2. (о разложении в ряд Фурье). Для всякой двоичной функции имеется единственное разложение вида: 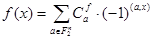 , где коэффициенты
, где коэффициенты 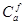 являются рациональными числами. При этом значения коэффициентов определяются равенствами
являются рациональными числами. При этом значения коэффициентов определяются равенствами
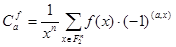 .
.
Доказательство. Докажем сначала, что указанный ряд представляет функцию 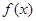 . Имеем
. Имеем 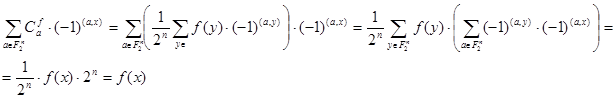
Поскольку в последней сумме будет только одно нулевое слагаемое при y=x.
Покажем теперь, что коэффициенты 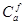 однозначно определяются по функции
однозначно определяются по функции 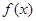 . Предположим, существует другое разложение
. Предположим, существует другое разложение 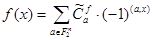 . Тогда
. Тогда 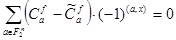 . Домножив обе части этого равенства на
. Домножив обе части этого равенства на 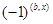 для
для 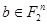 и просуммировав по
и просуммировав по 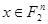 полученные равенства, получаем:
полученные равенства, получаем: 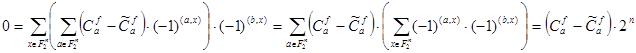
Отсюда 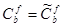 . Так как b-произвольный вектор из
. Так как b-произвольный вектор из 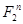 получаем требуемое утверждение.
получаем требуемое утверждение.
Определение 2.3.2. Коэффициенты 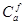 ,
, 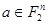 , называется коэффициентами Фурье функции
, называется коэффициентами Фурье функции 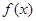 .
.
 2014-02-09
2014-02-09 1394
1394








