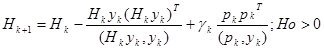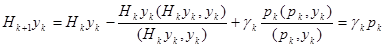2014-02-09
961
Метод тяжелого шарика:
Общий вид метода тяжелого шарика:
xk+1= xk - aÑf(xk)+b(xk-xk-1)
Это разностное уравнение, полученое из ДУ, которое описывает движение шарика, катящегося по некоторой поверхности с постоянным трением.
Введение инерции r(xk-xk-1) увеличивает скорость сходимости.
Теорема (о скорости сходимости метода тяжелого шарика):
Пусть 0< l I £ Ñ2f(x) £ L I (сильная выпуклость)
0 £ b £ 1, 0< a < a(1-b)/L,
тогда существует с=const такая, что || xk - x* || £ cqk,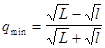 
Без доказательства
Таким образом, метод сходится не быстрее геометрической прогрессии, как и градиентный метод; показатель геометрической прогрессии тот же, только с корнями, но применение двухшагового метода при плохой обусловленности позволяет уменьшить эту обусловленность.
Модификаций двухшагового метода- метод сопряженных градиентов.
Метод сопряженных градиентов
xk+1 = xk - ak Ñf(xk) + bk (xk-xk-1)
Отличается тем, что ak и bk зависят от шага и выбираются следующим образом:
(ak , bk) = argmin f(xk - akÑf(xk)+bk(xk-xk-1))
{a,b}
Для квадратичной функции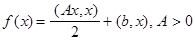 
|
|
|
1. Метод сходится за конечное число шагов, не превосходящее размерности пространства состояний.
2. Градиенты в методе попарно ортогональны (Ñf(xi), Ñf(xk))=0, "i¹k
Но в Rn не может существовать более n ортогональных ненулевых векторов, поэтому для некоторого k £ n будет Ñf(xk)=0, то есть точка xk- точка минимума.
3. Последовательные направления движения pk=xk-xk-1 удовлетворяют соотношению (Api, pj ) =0 "i¹j
Определение:
Векторы pi, связанные соотношением (Api, pj ) =0, называются сопряженными или А- ортогональными.
В методе сопряженных градиентов xk является точкой минимума квадратичной функции f(x) на подпространстве, порожденном первыми k градиентами. Следовательно никакой метод, использующий только градиенты функции (точнее, в котором шаг делается по линейной комбинации предыдущих градиентов), не может сходиться быстрее, то есть метод сопряженных градиентов является оптимальным по скорости сходимости в классе методов первого порядка.
Модификация Полака-Ривьера
xk+1= xk+ akpk, где ak = argmin f(xk+ akpk ), a>0
pk= -Ñf(xk)+bkpk-1
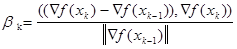b0 = 0
Для квадратичной функции последовательность точек xi , определенная этими формулами, совпадает с последовательностью, полученной методом сопряженных градиентов.
Эту модификацию удобнее применять для произвольных (неквадратичных) функций.
Рекомендуется применять процедуру обновления, т.е. через каждые n-шагов происходит сдвиг в направлении антиградиента.
То есть b0 = 0, затем bn=0...... bmn=0, следовательно pk= -Ñf(xk)+0*pk-1= -Ñf(xk)
(сдвиг в направлении антиградиента)
По скорости сходимости n шагов метода сопряженного градиента эквивалентны одному шагу метода Ньютона (для квадратичной функции метод сходится за один шаг).
|
|
|
1.4.Квазиньютоновские методы
общая структура: xk+1 = xk - gkHkÑf(xk)
1. Если Hk =I, то это градиентный метод.
2. Если Hk = (Ñ2f(xk))-1, то это метод Ньютона.
3. Если Hk = Hk (Ñf(xi), i=1..k) ® (Ñ2f(xk))-1, т.е. матрица Hk пересчитывается рекурентным способом на основе информации, полученной на k-й итерации.
Достоинство:
Не надо вычислять обратную матрицу вторых производных.
Обозначим pk = HkÑf(xk)
yk= Ñf(xk+1) -Ñf(xk),
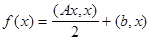,A>0
Тогда для квадратичной функции имеем
yk = A(xk+1-xk) = gkApk
gk pk = ykA-1,
поэтому матрицу Hk+1 (необязательно для квадратичной функции) выбирают так, чтобы выполнялось так называемое квазиньютоновское условие:
Hk+1yk= gkpk (Hk- должна стремиться к (Ñ2f(xk))-1
|
Проверим выполнение квазиньютоновского условия:
|
Для квадратичной функции метод сходится за n шагов, где n – размерность пространства состояний. Скорость сходимости этого метода сверхлинейная (быстрее любой геометрической прогрессии).Сходимость глобальная.
Объединяет достоинства градиентных методов и метода Ньютона.
Процедура применения:
На очередном шаге, имея Hk, делаем шаг в направлении pk. Получаем gk (например, по методу наискорейшего спуска), получаем xk+1 , вычисляем yk и пересчитываем Hk+1 для следующего шага.
Недостаток:
(по сравнению с методом сопряженных градиентов)
Надо хранить и пересчитывать Hk размерности m´n.
Метод Бройдена-Флетчера –Шенно.
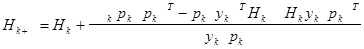
где
Примечание:
Последовательности xk, генерируемые каждым вариантом, для квадратичной функции совпадают. Существует много других модификаций приведенных квазиньютоновских методов.
1.5 Методы нулевого порядка
1. Методы апроксимации
В их основе лежит апроксимация градиента и матрицы вторых производных с помощью конечных разностей.
Пусть ej - орт j-й оси.
f (x + gej)» f(x) + ¶f/¶xjg + O(g2)
¶f/¶xj = (f(x + gej) - f(x))/ g» (f(x + gej) - f(x - gej))/ (2g)
Здесь под градиентом понимается конечная разность. Если g слишком мала, то слишком велики погрешности при вычислении производных. Если g велика, то из-из O(g2) погрешности тоже велики. Таким образом проблема этих методов- выбор g.
