Без доказательства
Пусть f(x) имеет вид: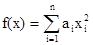 , где ai>0 сильно различаются между собой. Поверхности уровней функции вытянуты вдоль тех осей xi, которым соответствуют малые ai.
, где ai>0 сильно различаются между собой. Поверхности уровней функции вытянуты вдоль тех осей xi, которым соответствуют малые ai.
Для более эффективного применения градиентных методов необходимо превращение поверхностей уровня в круги



 x0
x0
 |  | ||||
 | |||||
Заменой переменных 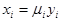 можно добиться того, чтобы у новых переменных yi поверхности уровней стали сферами. Для этого достаточно принять
можно добиться того, чтобы у новых переменных yi поверхности уровней стали сферами. Для этого достаточно принять 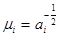 (все коэффициенты квадр. формы- единицы)
(все коэффициенты квадр. формы- единицы)
В случае, когда f(x) не квадратичная, а достаточно гладкая функция общего вида выбирают :
:
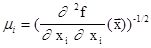
Это диагональные элементы матрицы вторых производных. Это преобразование не превратит поверхности уровня в сферы, но в некоторых случаях позволит уменьшить их вытянутость. Гарантировано исправить топографию функции f(x) можно, если учесть все, а не только диагональные элементы матрицы вторых производных и преобразования координат вида:
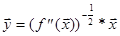
 2014-02-09
2014-02-09 470
470








