Метод наискорейшего спуска

Без доказательства.

Градиентный метод с дроблением шага.

Как известно выбор постоянного шага может привести к осложнениям.

x_k+1 = x_k - t_k*Ñf (x _k )-градиентный метод. Если шаг выбрать с условием, что f(x_k+1) - f(x_k) £ -e_* t_{k *} || Ñf(x_k)|| (*), где 0 £ e < 1, то результат будет лучше значительно.

Иллюстрация:

Необходимо двигаться к х*. В начальной точке проводим касательную к линии уровня и делаем по перпендикуляру к касательной в этой точке, шаг соответствующей величины. Если оказываемся «далеко», то делим шаг пополам, проводим линию уровня, касательную и шагаем по перпендикуляру и т.д.

Алгоритм:

1.Выбираем t=const.

2.Проверяем выполнение соотношения (*).

3.Если выполняется, то вычисляем следующую точку; если не выполняется, тогда длину шага t делим на 2, проверяем (*) и так далее.

Там, где Ñf (x) = 0- останавливаемся.

Теорема (о градиентном метоле с дроблением шага)

Градиентный метод с дроблением шага обеспечивает геометрическую скорость сходимости в точке минимума || x_k –x^*|| £ const._*q^k, где 0<q<1.

Определяет оптимальное значение шага на каждом такте.

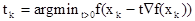
Значение функции, полученное этим методом, меньше чем в предыдущем методе.

Характерная черта метода: градиенты функции в соседних точках ортогональны.

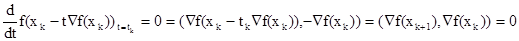
Графическая интерпретация:

В начальной точке проводим касательную к линии уровня и делаем шаг оптимальной величины в направлении перпендикуляра к касательной в данной точке. Получив новую точку, повторяем действия и так далее.

Теорема (о скорости сходимости метода наискорейшего спуска)

Скорость сходимости метода наискорейшего спуска - геометрическая.

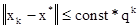, где (L, l -указаны ранее)