Градиентные методы (продолжение)

Без доказательства

x_k+1 = x_k - g_*Ñf (x _k )

Оценим скорость сходимости для выпуклых функций:

Теорема:

Пусть f (x) дваждыдифференцируема и l _*I £ Ѳf (x) £ L_*I, где l >0, L>0 "x (*),

то есть f (x) – выпукла, тогда при 0< g < 2/L выполняется неравенство:

|| x_k –x^*|| £ || x₀ –x^*||_*q^k – геометрическая сходимость,

где q = max {|1-g_* l |,|1-g_*L |}, при этом min q(g) = (L- l)/(L+ l)<1 и достигается при

g = g*=2/(L+ l).

Доказательство: Применим формулу

f (x+y)= f (x)+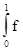¢(x+t_*y)y dt к производной:

Ñf (x_k)= Ñf (x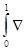^*) + ²f (x^*+t_*(x_k-x^*))(x_k-x^*) dt = A_k*(x_k-x^*),

где матрица A_k=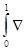²f(x^*+t_*(x_k-x^*))dt симметричная и неотрицательно определена.

Из (*) следует l _*I £ A_k £ L_*I,

|| x_k+1 –x^*|| = || x_k – g_*Ñf (x _k ) - x^*|| = || x_k – x^* - g_* A_k(x _k - x^*)|| =

= || (I- g_*A_k)_*(x _k - x^*)|| £ || I- g_*A_k ||_*|| x _k - x^*||

Для любой симметричной матрицы А выполняется:

|| I- A|| = max {|1-l₁|,|1-l_k|}, где l₁,l_k ­– соответственно наименьшее и наибольшее собственные числа (значения) матрицы А.

Поэтому || x_k+1 –x^*|| £ || x_k –x^*||_*q, где q = max {|1-g_* l |,|1-g_*L |}

так как 0< g < 2/L и 0< l <L, то |1-g_* l | <1, |1-g_*L |<1 Þ q<1.

Найдем min q(g)

q(g)

max =q(g)

ï1-g l ï

ï1-g l ï

1

L^-1g* l ^-1 g

1- l _*g^*= -(1-Lg^*) Þ g*=2/(L+ l).

Тогда q(g*) = (L- l) / (L+ l)