Отношения
Отношения являются сущностью и основным объектом исследования математики.
Пусть задано множество А (конечное или бесконечное), введем понятие декартова произведения – А ´ А, которое представляет собой множество всех пар D 2={< аi, aj >}, где (i, j) = 1, 2, 3, …, (ai, aj) Î A, и допускается i = j. Говорят, что Д2 задает декартово пространство, элементами которого являются все возможные пары. Любое подмножество a Í А ´ А = Д2 называется бинарным отношением. Заметим (и это важно), «a» также является множеством.
Пример 1.3. Авиационные трассы. Пусть A = { a, b, c, d, e }– множество кодов городов, для определенности a – Астрахань, b – Волгоград, c – Самара, d – Дудинка, е – Екатеринбург. На рис. 1.1 показано декартово пространство в виде двумерной решетки, узлы которой суть все возможные пары городов
Множество пар a = { ас, са, ав, ва, се, ес, ве, cd, de }, a Ì A ´ A можно назвать отношением с интерпретацией «город i непосредственно связан с городом j авиатрассой». На риc. 1.1 а) пары выделены «*». Бинарное отношение может быть изображено графом, в котором вершины суть элементы алфавита «А», а дуги соответствуют выделенным парам < i, j > отношения a,направление дуги указывается стрелкой от «i»к «j». Для примера 1.3 на рис. 1.1 б) построен соответствующий граф, задающий отношение a.
Математика имеет дело только с отношениями, например, уравнения и неравенства являются отношениями.
Пример 1.4. Линейное уравнение y = 0.5 x + 1 есть бинарное отношение 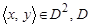 , где D – множество действительных чисел. Пары
, где D – множество действительных чисел. Пары 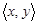 лежат на прямой y = 0.5 x и только на ней. На рис. 1.2 а) показан график этого отношения. На рис. 1.2 б) в пространстве Д ´ Д выделено отношение, заданное системой неравенств
лежат на прямой y = 0.5 x и только на ней. На рис. 1.2 а) показан график этого отношения. На рис. 1.2 б) в пространстве Д ´ Д выделено отношение, заданное системой неравенств 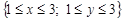 ; оно состоит из всех точек (пар,
; оно состоит из всех точек (пар, 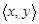 , попавших в заштрихованный квадрат.
, попавших в заштрихованный квадрат.
Отношения любой «арности» (п –арные отношения) определяются на соответствующих декартовых произведениях – А ´ А = = А 2, А ´ А ´ А = А 3, … А ´ А ´ … ´ А = Аn. По определению А 1 = А (само множество), А 0 = Æ (пустое множество).
Пример 1.5. Пусть задано уравнение xn + yn= zn, где x, y, z, n Î N. На N 4 = N ´ N ´ N ´ N выделяются четверки <x, y, z, n> Î N 4, которые задают отношение «быть решением уравнения 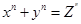 . Проблема нахождения таких четверок сформулирована в теореме Ферма.
. Проблема нахождения таких четверок сформулирована в теореме Ферма.
a) Декартово пространство б) Граф авиатрасс
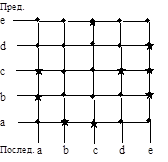
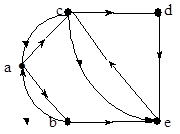
в) Дерево достижимости 2-го
порядка из вершины «а»
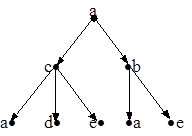
Рис. 1.1. Авиационные трассы. Математическая модель.
 2014-02-09
2014-02-09 393
393








