Двойственность ЗВП

В формулировке теоремы Куна- Таккера прямые и двойственные переменные входят симметричным образом. Поэтому можно ожидать, что аналогичная симметрия существует и для задач оптимизации относительно прямых и двойственных переменных.

Введем функцию: g(x)=sup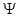(x,), при 0

Тогда очевидно,что

g(x) = f(x), если g_i(x)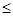0, i=1...m

g(x) =, в противном случае

Понятно, что 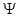(x,) = f(x)+(, g(x)),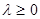

Поэтому исходная ЗВП может быть записана в виде:

min g(x)-?, при x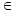Rⁿ

Эту задачу принято называть прямой.

Поступим аналогичным образом, поменяв роль переменных и операций max и min. Обозначим h()= inf 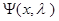, при xÎRⁿ

Задачу max h()-? при 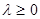, называют двойственной.

Теорема двойственности:

Справедливы следующие соотношения двойственности:

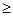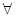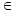1) f(x)h() xX,

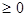
2) Если выполнено условие т. Куна-Таккера, а пара (x*,l*) является седловой точкой функции Лагранжа, то l*-решение двойственной задачи.

l* = argmax h(),при 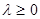и f(x*)=h(l*)

3)Если для допустимых x*, l*: f(x*)=h(l*), то

x* = argmin f(x), при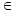 xX

l* = argmax h(), при 0

Доказательство:

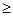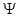1) f(x)f(x)+(,g(x))=(x,)inf(x,) = h(), при xÎRⁿ

2) Для всех 0 справедливо соотношение:

h(l*)= inf(x,l*) =(x*, l*)(x*,) inf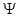(x,) = h(),при xÎRⁿ

Отсюда l*-решение двойственной задачи.

Но 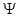(x, l*) = f(x*)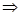h(l*)=f(x*)

3) На основании 1) f(x)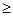h(l*) = (2)) f(x*)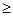h()

тогда x*- прямое решение, l*- двойственное решение

Продемонстрируем двойственность ЗВП на примере задачи линейного программирования (ЗЛП), которая вкладывается в ЗВП.

Напомним, что функция f называется вогнутой, если f выпуклая функция, которая выпукла и вогнута одновременно, является афинной или линейной функцией.