2014-02-09
3388
Классификация точек разрыва.
Определение. Точка разрыва 1 рода – это точка разрыва, в которой функция имеет конечные правый и левый пределы.
Пример.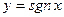 
,
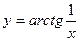
Определение. Если правый и левый пределы в т.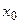 
равны между собой, то т. 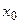- точка устранимого разрыва. Обычно в этой точке функция или не определена, или имеет предел, отличный от значения в этой точке. Чтобы устранить разрыв, нужно положить в этой точке значение функции равное пределу в этой точке.
Определение. Точка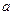 
называется точкой разрыва 2 рода, если в этой точке 
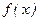не имеет по крайней мере одного из односторонних пределов.
Пример.
1. 
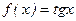при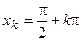 
; 
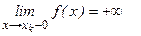
2. 
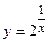
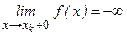
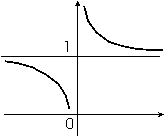
Существует теорема (доказывается в более подробных курсах анализа) о том, что: Все элементарные функции непрерывны в тех интервалах, на которых они определены.
Основные элементы функции:
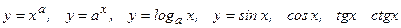,обратные тригонометрич. функции.
Функции, построенные из основных, при помощи конечного числа арифметических действий и операций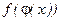 
называются элементарными.
Теорема. Пусть 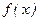и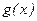 
заданы на одном и том же множестве 
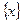и непрерывны в точке. .
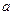Тогда функции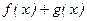 
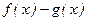
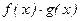
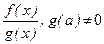тоже непрерывна в точке. .
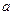Доказательство.
Т. к. непрерывные в точке 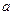функции имеют пределы в т. 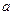, соответственно равные 
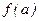и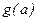 
, то по теореме о пределах, пределы перечисленных функций существуют и равны: 
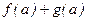,…., а это и есть значения функций в этих точках, следовательно, функции непрерывны в т. 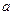по определению непрерывности.
