Пусть точка 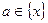 -области определения функции и любая
-области определения функции и любая 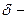 окрестность содержит отличные от
окрестность содержит отличные от 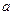 значения
значения 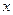 .
.
Определение. Функция 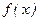 называется непрерывной в точке
называется непрерывной в точке 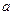 , если
, если
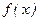 имеет в т.
имеет в т. 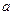 предел и этот предел равен значению функции в т.
предел и этот предел равен значению функции в т. 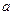 .
.
т.е. 
Определение. 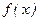 – непрерывна в т.
– непрерывна в т. 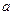 , если
, если 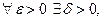 что
что 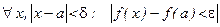 т. к.
т. к. 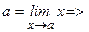 (
(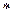 )
) 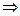
 , т. е. для непрерывной функции в т.
, т. е. для непрерывной функции в т. 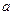 можно менять местами символ
можно менять местами символ 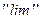 и
и 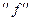
Определение. 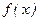 называется непрерывной в т.
называется непрерывной в т. 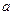 справа (слева), если правый (левый) предел этой функции в т.
справа (слева), если правый (левый) предел этой функции в т. 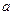
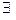 и равен
и равен 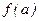
Запись: 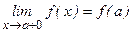 или
или 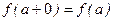
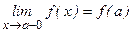 или
или 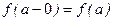
Определение. Если 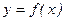 непрерывна в каждой точке некоторого интервала
непрерывна в каждой точке некоторого интервала 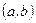 , где
, где 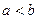 , то говорят, что она непрерывна на интервале
, то говорят, что она непрерывна на интервале 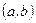 .
.
Определение. Если 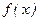 непрерывна в каждой точке интервала
непрерывна в каждой точке интервала 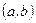 и на концах этого интервала, (справа и слева), то, следовательно, она непрерывна на отрезке
и на концах этого интервала, (справа и слева), то, следовательно, она непрерывна на отрезке  .
.
Пример 1. 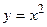 непрерывна на любом отрезке
непрерывна на любом отрезке  .
.
Пример 2.  (разрывается на отдельные кривые в т.
(разрывается на отдельные кривые в т. 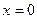 )
)
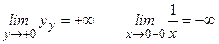
Пример 3. 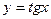 (в т.
(в т. 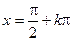 )
)
Пример 4. 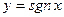 (в т.
(в т. 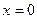 )
) 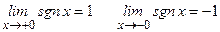
Все эти точки называются точками разрыва.
Определение. Если для функции 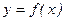 в т.
в т. 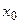 нарушается условие непрерывности, то
нарушается условие непрерывности, то 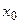 - точка разрыва.
- точка разрыва.
Это значит: 1. Или предел бесконечен или не существует.
2. Либо предел существует, но не равен 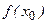 .
.
 2014-02-09
2014-02-09 594
594







