По определению: 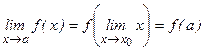 .
.
Правило 1. Для того, чтобы найти предел элементарной функции, когда 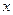 стремится к значению, лежащему в интервале, в котором функция определена, нужно в выражение функции подставить вместо
стремится к значению, лежащему в интервале, в котором функция определена, нужно в выражение функции подставить вместо 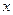 его предельное значение.
его предельное значение.
Случай 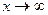 или значение не принадлежит области определения, требуют специального рассмотрения.
или значение не принадлежит области определения, требуют специального рассмотрения.
Пример. 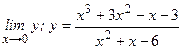
1. 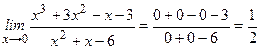

2. 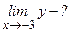 знаменатель равен 0, но
знаменатель равен 0, но 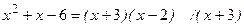
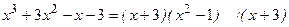
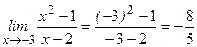
3. 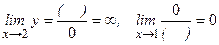
Правило 2. Если существует 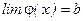 , а
, а 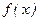 – непрерывна в точке
– непрерывна в точке 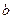 , то
, то
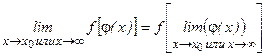
Пример. 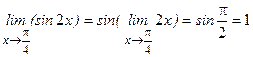
 2014-02-09
2014-02-09 469
469







