Некоторые определения и понятия линейной алгебры

Кандидат юридичних наук Іваньков І.В.

Определение. Пусть 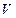- некоторое векторное пространство. Функция

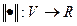
называется векторной нормой, если для 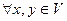виполняются следующие условия:

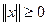1. - неотрицательность; при этом

.

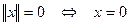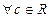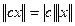1. : - однородность;
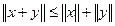2. - неравенство треугольника.

Пример. 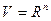, т.е. если 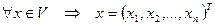. Можно ли задать векторную норму следующим образом: ?

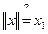Для того, чтобы ответить на поставленный вопрос, необходимо проверить, выполняются ли условия 1-3 предыдущего определения для функции 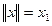. Уже при проверке первого условия очевидно его нарушение. Действительно, если, например, 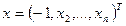, то для такого вектора 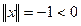. Таким образом, задать норму функцией 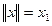нельзя.

Пример. 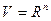. Можно ли задать векторную норму следующим образом: ?

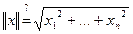Проверим выполнение условий 1-3.

1. ;

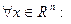
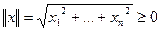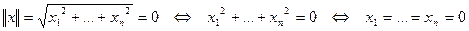- первое условие выполнено.

2. 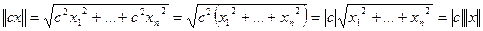- второе условие выполнено.

3. Доказать самостоятельно.

Таким образом, функция 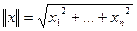действительно определяет векторную норму (это хорошо известная евклидова норма).