Примеры векторных норм

Вектор .

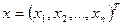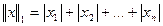1. - первая векторная норма;
2. - -норма;
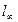3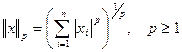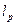. - -норма или норма Гёльдера с показателем .

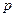Определение. Пусть 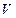- некоторое векторное пространство. Функция

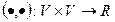
называется скалярным произведением, если для 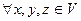виполняются следующие условия:

1. - неотрицательность; при этом

.

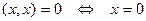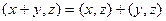1. - аддитивность;
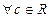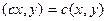2. : - однородность.

Определение. Пусть 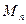- матричное пространство (матрицы размером ). Функция

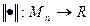
называется нормой матрицы, если 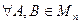виполняются следующие условия:

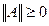1. - неотрицательность; при этом

.

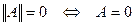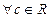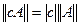1. : - однородность;
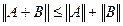2. - неравенство треугольника;
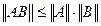3. - кольцевое свойство.

Задание. Доказать: 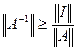, где 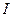- единичная матрица соответствующей размерности.