2014-02-09
546
1. 
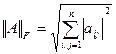- норма Фробениуса;
2. 
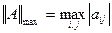- max-норма;
3. 
;
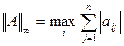4. 
;
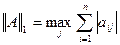5. 
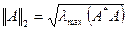- спектральная матричная норма, где 
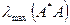- максимальное собственное значение матрицы 
.
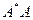Определение. Пусть 
- векторная норма на пространстве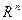 
. Матричная норма на 
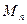, определяемая формулой
,
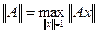называется подчиненной, или согласованной с рассматриваемой векторной нормой.
Определение. Матрица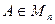 
называется положительно определенной, если для 
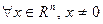выполняется:
.
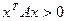Пример. Показать, что матрица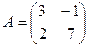 
является положительно определенной. Поскольку 
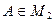, то произвольный вектор 
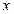из предыдущего определения берется из пространства 
: 
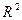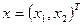. Рассмотрим конкретный вид 
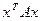для заданной матрицы:
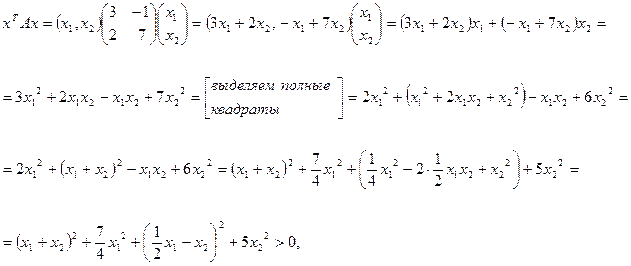
откуда вытекает, что исходная матрица является положительно определенной.
Критерий Сильвестра положительной определенности матрицы. Для того, чтобы матрица 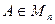была положительно определенной, необходимо и достаточно, чтобы определители всех ее главных подматриц были положительными.
Для предыдущего примера у матрицы 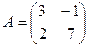есть две главные подматрицы: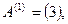 
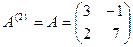, при этом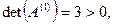 
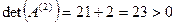, что говорит о положительной определенности матрицы в соответствии с критерием Сильвестра.
