Методы одномерной оптимизации

Постановка: требуется оптимизировать х (формальная постановка)

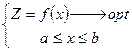
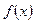- функция одной переменной

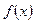- целевая функция.

Решение: найти х, при котором 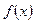принимает оптимальное значение.

2 варианта:

- минимизировать – задача минимизации;

- максимизировать – задача максимизации.

Рассмотрим случай минимизации

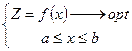
2 способа:

- аналитический

- численный

В аналитическом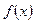задается в виде формулы, в численном 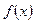задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.

Пусть функция определена в некоторой области S (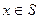), в случае одномерной оптимизации S – интервал :

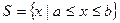1. точка 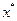называется глобальным минимумом, если для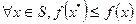
2. точка 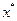называется строгим глобальным минимумом, если для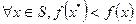
3. точка 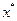называется локальным минимумом, если для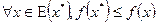
4. точка 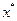называется строгим локальным минимумом, если для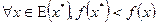

Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.