2014-02-09
337
Аналитический способ нахождения локального минимума.
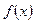- дифференцируема
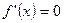- необходимое условие точки локального минимума.
 | |||
 | |||
 |
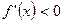
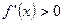
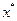
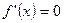
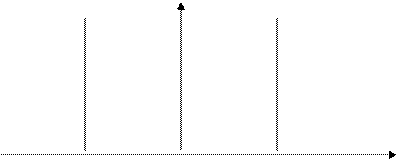
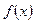Пусть функция задана на интервале 
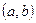, при этом существует такая точка 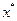, что на 
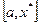– монотонно убывает, а на 
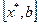– монотонно возрастает, то функция унимодальная.
 |
а 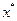b
Если из того что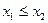 
следует, что 
, то функция называется монотонно возрастающей. Если из того что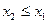 
следует, что 
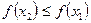, то функция называется монотонно убывающей.
