Метод Гауса

Математическое моделирование задачи.

Различают другие типы задач:

1) задачи о диете или о рациональном питании.

2) задачи производственного планирования

3) на составление математического моделирования

4) задачи о раскрое

5) задачи о назначениях.

М.Г. вычисляется с помощью таблиц Гауса.

2х1-х2+х3=3

х1+3х2-2х3=1 разрешающий элемнт.

х2+2х3=8 разрешающая строка разреш.столбец.

Х1	Х2	Х3	Св.чл		проверка
	-1
		-2
	-7			-1	-1
		-2
		-8	-23	-30	-30

1)разрешающую строку делим на разрешающий элемент. 2) в разрешающем столбце элементы заменяем на ноли. 3) Все остальные элементы таблицы считаются по правилу прямоугольника.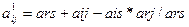

переход от одной формы модели к другой форме модели, различные формы моделей З.Л.П.

В зависимости от системы ограничения различают в Л.П. три формы модели 1) каноническая 2) стандартная форма 3) общая форма. Эти три формы эквиваленты между собой в том смысле, что от одной формы можно перейти к другой с помощью элементарных преобразований.

Стандартная форма модели З.Л.П.. Система задачи формируется: Найти вектор х, удовлетворяющий системе ограничений и условию не отрицательности.

а11х1+а12х2+…+а1nxn<=b1

a21x1+a22x2+…+a2nxn<=b2

….

am1x1+am2x2+…+amnxn<=bn

xj>=0 j=1,4; Z=c1x1+c2x2+..+cnxn->max

A-матрица (m*n) Z=cx->max Ax<=b x>=0; C=(C1 C2 …Cn) b(b1 b2..bm)

Каноническая тоже самое только в системе ограничений = и Ax=b.

Общая форма. Найти вектор Х, удовлетворяющий системе ограничений

a11x1+a12x2+...+a1nxn=b1

am1x1+amnxn=bm

Xj>=0 (j=1,l) l<n Для которого Z=с1х1+cnxn -> max

Для того что бы решать задачи Л.П. симплекс методом необходимо иметь каноническую форму модели, поэтому необходимо знать, как перейти от одной формы модели к другой.