Статвес определяет состояние системы, но не является единственной величиной. Покажем это: разделим объём на две части. Тогда 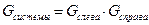 , т.е. статвес не является аддитивной величиной.
, т.е. статвес не является аддитивной величиной.
Но, можно взять 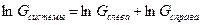 . Тогда энтропия (формула Больцмана):
. Тогда энтропия (формула Больцмана):
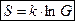
где 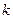 - постоянная Больцмана.
- постоянная Больцмана.
При максимальном статвесе, энтропия тоже максимальна. При необратимом процессе, система переходит из менее в более вероятное состояние, при этом увеличивается статвес, а значит и энтропия.
Находясь в равновесии, энтропия может кратковременно уменьшаться, но её можно считать постоянной в равновесии.
Закон возрастания энтропии (2-е начало термодинамики).
Энтропия в замкнутой изолированной системе (системе, предоставленной самой себе), может только возрастать или, достигнув своего максимального значения, оставаться постоянной.
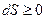 .
.
Статистической физикой доказано, что если системе сообщается некое количество теплоты 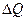 , то в ходе обратимого (обратимым является только изотермический процесс) процесса, энтропия:
, то в ходе обратимого (обратимым является только изотермический процесс) процесса, энтропия:
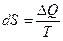 .
.
Энтропия является функцией состояния (зависит от параметров системы). Поэтому, для круговых процессов энтропия:
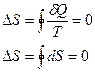 .
.
Состояние, которое осуществляется малым числом способов, называется упорядоченным; если большим числом, то беспорядочным. Поэтому, энтропия – это мера беспорядка в системе.
При сообщении системе кого-то количества теплоты, увеличивается мера беспорядка из-за теплового движения, т.е. увеличивается число микро и микросостояний, реализующих данное макросостояние, т.е. увеличивается статвес, а значит и энтропия.
Чес больше температура, тем больше внутренняя энергия системы, следовательно, тем меньше доля беспорядка, обусловленного сообщением системе количества теплоты 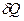 .
.
Возрастание энтропии в замкнутой системе соответствует увеличению хаотичности молекулярного движения, следовательно, система переходит в равновесное состояние, соответствующее полному беспорядку.
Вторая формулировка 2-го начала термодинамики:
При любых процессах, происходящих в изолированной системе, система переходит из менее в более вероятные состояния.
Если количество теплоты сообщается системе в ходе необратимого процесса, то возрастание энтропии обусловлено как сообщением количества теплоты, так и необратимостью процесса. Тогда
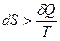 .
.
Для обратимого и необратимого процессов:
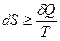 ,
,
где знак 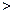 соответствует необратимому процессу, а знак равенства – обратимому.
соответствует необратимому процессу, а знак равенства – обратимому.
Поскольку энтропия – есть функция состояния, то её можно выразить через параметры состояния (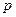 ,
, 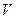 ,
, 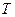 ).
).
Третье начало термодинамики:
При 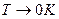 всего одно микросостояние реализует макросостояние (основное состояние), т.е.
всего одно микросостояние реализует макросостояние (основное состояние), т.е. 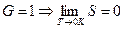 (теорема Нернста).
(теорема Нернста).
Выразим энтропию через параметры состояния:
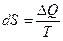 .
.
Из 1-го начала термодинамики:
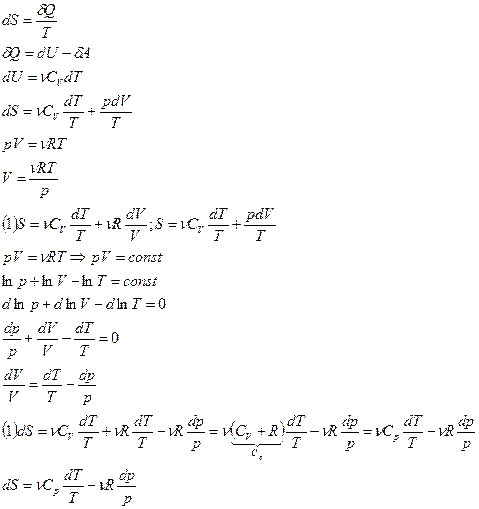 .
.
В физике часто используют 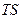 -диаграмму:
-диаграмму:
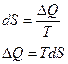 .
.

Изобразим в 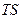 -координатах различные изопроцессы.
-координатах различные изопроцессы.
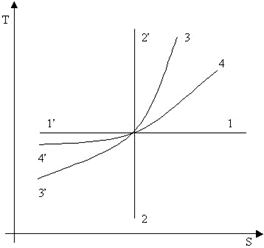
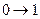
| 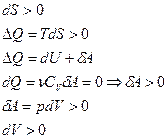 изотермическое расширение
изотермическое расширение
|
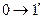
| 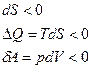 изотермическое сжатие
изотермическое сжатие
|
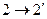
| 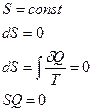 адиабатический процесс (изоэнтропийный)
адиабатический процесс (изоэнтропийный)
|
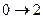
| 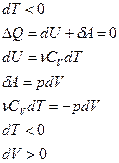 адиабатическое расширение
адиабатическое расширение
|
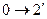
| 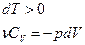 адиабатическое сжатие
адиабатическое сжатие
|
 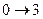
| 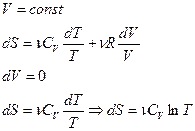
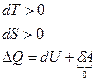 изохорное нагревание
изохорное нагревание
|
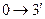
| 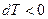 изохорное нагревание
изохорное нагревание
|
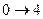
| 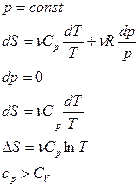
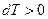 изобарное нагревание
изобарное нагревание
|
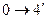
| 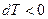 изобарное охлаждение
изобарное охлаждение
|
При циклическом процессе 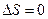 . Рассмотрим цикл Карно:
. Рассмотрим цикл Карно:
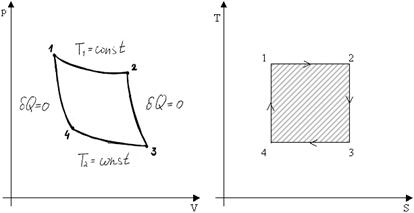
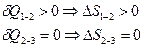
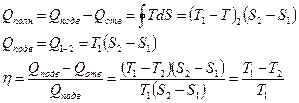 .
.
 2014-02-09
2014-02-09 756
756








