2014-02-10
656
Запишем векторное произведение двух векторов – оператора Гамильтона и гладкой векторной функции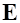 
. Эта операция порождает производное векторное поле, называемое ротором или вихрем поля :
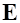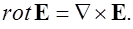
Ротор характеризует интенсивность и направление вихревого движения в векторном поле. Например, пусть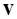 
- линейная скорость выделенного элемента твердого тела, вращающегося с постоянной угловой скоростью 
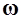. Тогда 
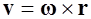. Расчет дает
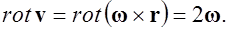
Выразим проекции вектора ротора в декартовой системе координат:
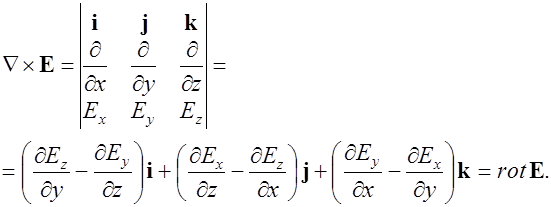
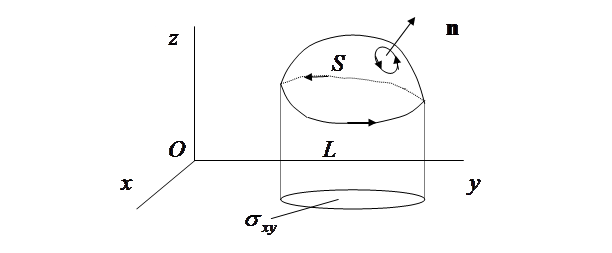
Формула Стокса дает выражение интеграла по поверхности через интеграл по замкнутому контуру, ограничивающему эту поверхность. Положительное направление нормали в любой точке поверхности составляет правый винт с направлением положительного обхода элементарного контура у этой точки. Направление обхода контура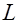 
согласовано с направлением положительного обхода каждого элементарного контура на поверхности 
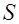. На рис 1.19 
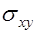- проекция поверхности 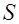на плоскость 
.
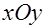Формула Стокса утверждает, что поток вихря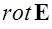 
векторного поля 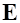через кусочно-гладкую поверхность 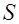, ограниченную замкнутым контуром 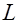, равен циркуляции вектора 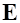по этому контуру.
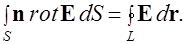(1.51)
