2014-02-10
4109
Основная задача электростатики.
Основная задача электростатики состоит в определении напряженности электрического поля по заданному распределению источников поля - неподвижных электрических зарядов. В общем случае решение такой задачи упрощается, если его проводить в два этапа:
1) сведение задачи к решению дифференциального уравнения для потенциала;
2) нахождение напряженности поля по уже найденному потенциалу.
Чтобы получить уравнение для потенциала, подставим выражение потенциала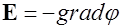 
в (1.60). Найдем
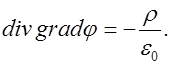(1.61)
Учтем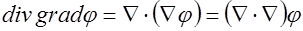 
. Скалярное произведение двух векторных операторов Гамильтона порождает скалярный дифференциальный оператор второго порядка – оператор Лапласа:
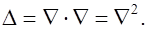(1.62)
В декартовых координатах оператор Лапласа записывается как
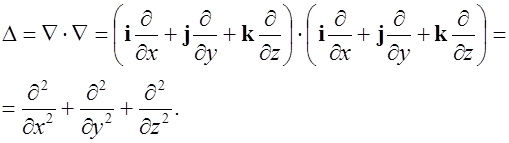(1.63)
С учетом (1.62) из (1.61) следует уравнение Пуассона
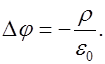(1.64)
После решения уравнения Пуассона (1.64) относительно потенциала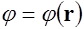 
по заданному распределению плотности заряда 
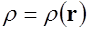можно найти напряженность поля 
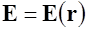по формуле .
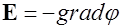При переходе от дискретного к непрерывному распределению зарядов формула
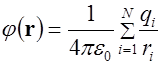(1.24)
для потенциала поля системы зарядов заменяется формулой
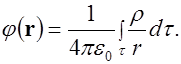(1.65)
Выражение (1.65) является решением уравнения Пуассона (1.64), если все заряды сосредоточены в объеме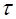 
конечной величины. Формулы (1.24) и (1.65) предполагают нормировку потенциала на нуль в бесконечности. Само уравнение Пуассона при решении не предполагает обязательного использования именно этой нормировки.
Решение основной задачи электростатики оказывается однозначным. Это следует из однозначности решения прямой задачи электромагнетизма о нахождении электромагнитного поля по заданным источникам поля, граничным и начальным условиям для поля.
Решение обратной задачи электростатики (нахождение распределения источников поля - зарядов по электрическому полю, заданному в конечном объеме) в общем случае неоднозначно.
Пример. Однородно заряженный шар создает вне своего объема такое же электрическое поле, как и точечный заряд, равный заряду шара и помещенный в точку центра шара.
Если в области пространства, где требуется найти электрическое поле, заряды отсутствуют (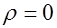
), то уравнение Пуассона (1.64) превращается в уравнение Лапласа
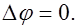(1.66)
Для решения уравнения Лапласа, как и уравнения Пуассона, должны быть заданы граничные условия для потенциала. Эти условия задаются на поверхности, ограничивающей область, где надо найти потенциал.
