Рис. 1.19. К формуле Стокса
Для электростатического поля, согласно (1.18),
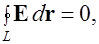 (1.18)
(1.18)
что ввиду произвольности выбора поверхности 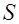 позволяет получить из (1.51):
позволяет получить из (1.51):
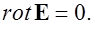 (1.52)
(1.52)
Если (1.18) – интегральная формулировка потенциальности электростатического поля, то (1.52) выражает то же условие в дифференциальной форме. Применение (1.52) при проверке потенциальности поля может оказаться более удобным, чем применение (1.18).
Приведем другой пример использования понятия ротора - для упрощения выражения
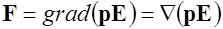 (1.50)
(1.50)
силы, действующей на диполь в неоднородном поле.
Пусть дипольный момент 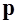 - постоянный, то есть
- постоянный, то есть 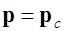 . Используем векторное тождество
. Используем векторное тождество
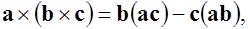
в котором положим 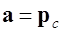 ,
, 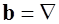 , и
, и 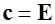 . Получим
. Получим
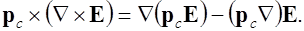
В силу потенциальности электростатического поля
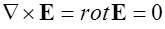 ,
,
отсюда
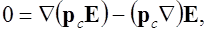
и
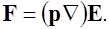
Пусть двусторонняя и кусочно-гладкая поверхность 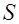 , замкнутая или незамкнутая, помещена в векторное поле
, замкнутая или незамкнутая, помещена в векторное поле 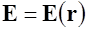 (см. рис. 1.20). Рассмотрим ее элемент
(см. рис. 1.20). Рассмотрим ее элемент 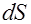 ,
, 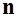 - единичная нормаль к площадке элемента
- единичная нормаль к площадке элемента 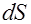 .
.
Определение. Потоком векторного поля 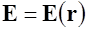 через элемент
через элемент 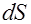 называется величина
называется величина 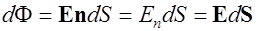 , где
, где 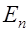 - проекция вектора
- проекция вектора 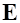 на направление нормали
на направление нормали 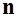 , и
, и 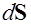 - вектор элемента площади,
- вектор элемента площади, 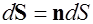 .
.
Имеем: 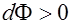 , если векторы
, если векторы 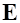 и
и 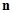 образуют острый угол,
образуют острый угол, 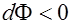 , если векторы
, если векторы 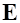 и
и 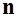 образуют тупой угол, и
образуют тупой угол, и 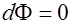 , если
, если 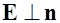 .
.
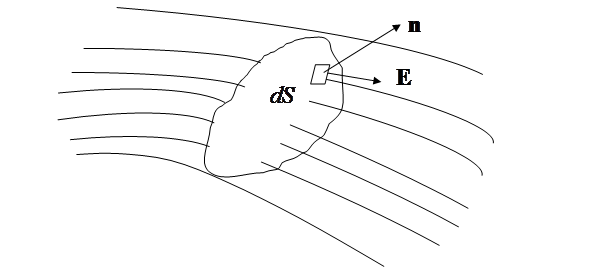
Рис. 1.20. Поток векторного поля через поверхность
Определение. Потоком векторного поля 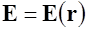 через всю поверхность
через всю поверхность 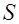 называется поверхностный интеграл
называется поверхностный интеграл
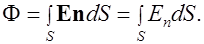 (1.53)
(1.53)
В наиболее простом случае векторные линии поля пересекают поверхность 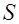 лишь один раз. Тогда величина потока
лишь один раз. Тогда величина потока 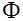 через поверхность
через поверхность 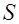 пропорциональна числу векторных линий поля, пересекающих ее.
пропорциональна числу векторных линий поля, пересекающих ее.
Выразим поток напряженности поля 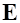 заряда
заряда 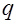 через сферу, в центре которой находится заряд
через сферу, в центре которой находится заряд 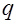 (см. рис. 1.21):
(см. рис. 1.21):
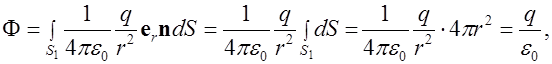
так как 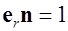 .
.
Силовые линии электрического поля в области, где нет зарядов, непрерывны. Число линий напряженности, пересекающих сферу 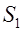 и произвольную поверхность
и произвольную поверхность 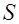 , охватывающую заряд
, охватывающую заряд 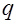 , одинаково. Поэтому поток поля
, одинаково. Поэтому поток поля 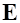 через сферу
через сферу 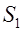 равен потоку того же поля через поверхность
равен потоку того же поля через поверхность 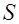 . Заряд
. Заряд 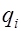 системы зарядов
системы зарядов 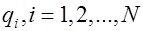 , находящихся в объеме
, находящихся в объеме 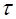 , ограниченным поверхностью
, ограниченным поверхностью 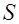 , создает поток
, создает поток 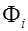 через поверхность
через поверхность 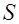 . В соответствии с принципом суперпозиции поток поля
. В соответствии с принципом суперпозиции поток поля 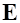 системы зарядов через поверхность
системы зарядов через поверхность 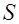 равен алгебраической сумме потоков
равен алгебраической сумме потоков 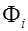 полей
полей 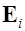 отдельных зарядов системы в объеме
отдельных зарядов системы в объеме 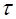 , ограниченном поверхностью
, ограниченном поверхностью 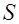 :
:
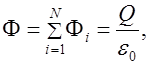 (1.54)
(1.54)
где 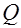 - заряд системы,
- заряд системы, 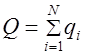 ,
, 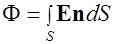 ,
, 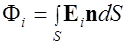 ,
, 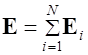 .
.
Для непрерывной модели распределения зарядов с объемной плотностью 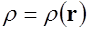 заряд в объеме
заряд в объеме 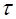 равен
равен 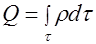 , что и следует учитывать при использовании формулы (1.54).
, что и следует учитывать при использовании формулы (1.54).
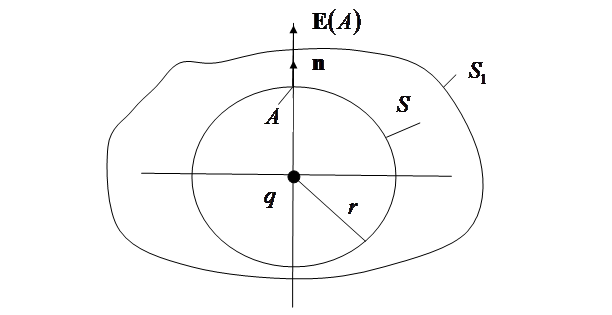
Рис. 1.21. К теореме Гаусса, 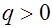 ,
,
для замкнутой поверхности единичная нормаль 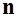 выбирается внешней
выбирается внешней
Формула (1.54) выражает теорему Гаусса для электростатического поля в интегральной форме:
Поток напряженности электрического поля через замкнутую поверхность равен электрическому заряду в объеме, ограниченном этой поверхностью, деленному на 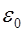 .
.
Выводы:
1) Теорема Гаусса выражает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом в объеме, ограниченном этой поверхностью.
2) Физической основой теоремы Гаусса является закон Кулона. Иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
Теорема Гаусса позволяет найти полный заряд в объеме посредством измерения потока напряженности через поверхность, ограничивающую объем. Другие способы определения заряда не дают удовлетворительного результата. Применению других методовпрепятствует то, что закон распределения измеряемого заряда в объеме заранее не известен. Исключение составляет метод, когда измеряемый заряд помещается в однородное электрическое поле напряженностью 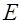 . Измерив силу
. Измерив силу 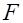 , действующую на заряд со стороны поля, можно найти искомый заряд
, действующую на заряд со стороны поля, можно найти искомый заряд 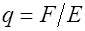 .
.
 2014-02-10
2014-02-10 901
901








