Особенности спектрального анализа в цепях с нелинейными реактивными элементами

Рис. 3.2

График тока имеет характерный вид периодической последовательности косинусоидальных импульсов с отсечкой. Искомая последовательность выражается аналитически при подстановке (3.6) в (3.5) как:

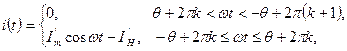(3.7)

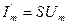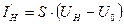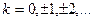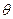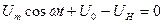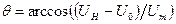где , , , - параметр, называемый углом отсечки и определяемый из условия: как при 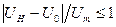(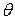равно половине части периода колебаний, когда протекает ток).

Спектр тока выражается формулой (3.3), где амплитуды компонент спектра находятся при подстановке (3.7) в выражения для этих коэффициентов, данные после (3.3):

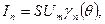(3.8)

где 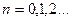, 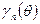- функция Берга 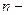ого порядка,

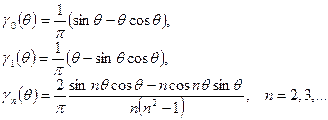
Для получения максимально возможного значения амплитуды с номером 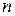надо соответствующим образом выбирать .

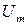Пример. Нелинейный элемент имеет кусочно-линейную ВАХ с параметрами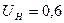В, 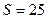мА/В. К данному элементу приложено напряжение 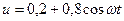, В. Вычислить постоянную составляющую 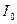и амплитуду первой гармоники тока .

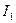Так как 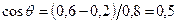, то 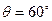. Значения функций Берга:

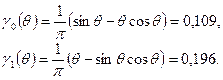
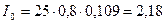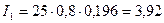По формулам (3.8) имеем мА, мА.

Степенная аппроксимация. На ее применении основан метод с использованием тригонометрических формул кратного аргумента. Пусть в окрестности рабочей точки 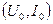вольт-амперная характеристика нелинейного элемента представлена в виде:

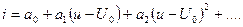(3.9)

Приложенное к двухполюснику напряжение дается выражением (3.6). Используя известные формулы:

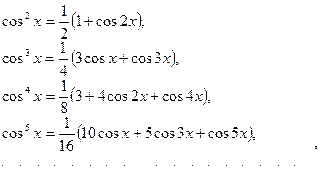
путем подстановки (3.6) в (3.9) получим выражение для спектра тока:

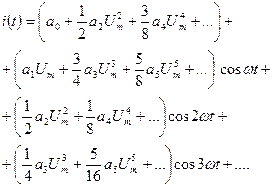(3.10)

Из (3.10) следует общее выражение для амплитуды тока гармоники с номером :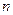

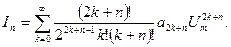(3.11)

Вывод: постоянная составляющая и амплитуды четных гармоник определяются коэффициентами степенного ряда с четными номерами. Амплитуды нечетных гармоник зависят лишь от нечетных коэффициентов.

Пример. Рассмотрим нелинейные искажения в транзисторном усилителе с резистивной нагрузкой 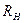, показанном на рис. 3.3.

Полагаем, что амплитуда 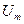входного гармонического сигнала достаточно велика, чтобы вызвать необходимость учета нелинейности проходной характеристики транзистора 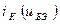. Аппроксимируем характеристику в окрестности рабочей точки полиномом второй степени:

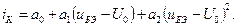
На вход усилителя подается напряжение

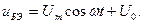
В коллекторной цепи получим спектр тока, содержащий постоянную составляющую, а также первую и вторую гармоники с амплитудами (см. (3.11)):

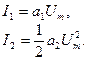
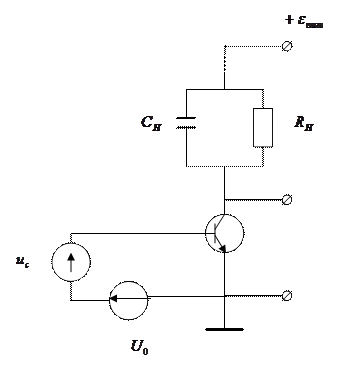Рис. 3.3

Эти гармоники тока, проходя через резистор нагрузки 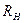, создают на нем падение напряжения, которое является выходным сигналом. Уровень нелинейных искажений на выходе усилителя оценим, найдя коэффициент нелинейных искажений (3.4). В данном случае

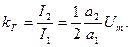
Заметим, что коэффициент нелинейных искажений увеличивается с ростом амплитуды входного сигнала .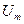

Показательная аппроксимация. Здесь применяется метод, основанный на использовании функций Бесселя мнимого аргумента. Если ВАХ двухполюсника аппроксимирована выражением

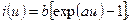(3.12)

для вычисления спектра тока используют формулу

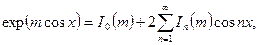
где 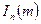- модифицированная функция Бесселя 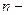ого порядка.

Пусть на двухполюсник действует напряжение (3.6). Спектр тока выражается формулой (3.3), где амплитуды компонент спектра находятся при подстановке (3.12) в выражения для этих коэффициентов, данные после (3.3). В результате получим спектр тока:

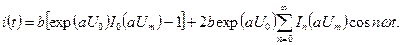(3.13)

Аппроксимация точного решения спектральной задачи в виде разложения (3.3) конечным числом 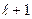первых членов этого разложения:

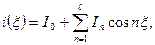(3.14)

где .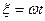

На основе аппроксимации (3.14) разработан приближенный графо-аналитический метод спектрального анализа колебаний. Он широко применяется для оценки нелинейных искажений в усилителях, модуляторах и т.д. В отличие от уже изученных методов он не требует знания аппроксимации ВАХ нелинейного элемента. Пусть на элемент подается напряжение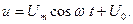

Метод пяти ординат позволяет оценить постоянную составляющую тока и амплитуды первых четырех его гармоник. Тогда в (3.14) полагают 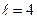. Для пяти моментов времени, когда 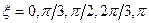, соответственно, находят значения входного напряжения. Графически находят пять ординат ВАХ, которые соответствуют этим пяти точкам входного напряжения: 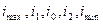(см. рис. 3.4). При этом расстояния между точками на оси абсцисс (оси напряжения 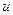) оказываются одинаковыми.

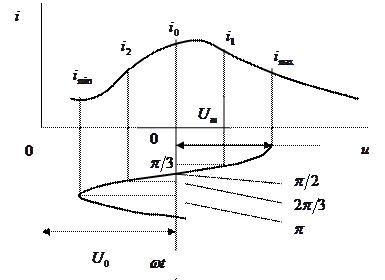Рис. 3.4 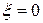при , (),(),(),(),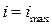

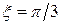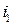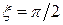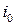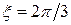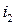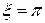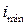Искомые постоянная составляющая 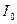и амплитуды первых четырех гармоник спектра тока: 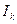, , 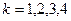находят из условия, что ординаты пяти точек, найденные на ВАХ, удовлетворяют в соответствующие моменты времени уравнению (3.14). Получим систему линейных уравнений:

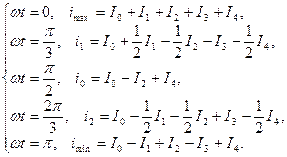(3.15)

Решая систему (3.15), найдем искомые величины:

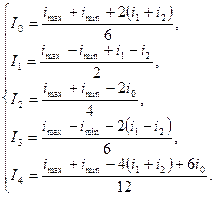(3.16)

Метод трех ординат - менее точный, но более простой в реализации, чем изученный метод пяти ординат. Для него в (3.14) 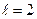. Заданы три момента времени, для которых 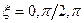. Для них ищут графически три точки на ВАХ элемента. Расчетные формулы имеют вид:

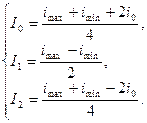(3.17)

Аппроксимация с помощью ряда Тейлора. В некоторых случаях функциональная зависимость ВАХ может быть сложной. Разложение этой зависимости в ряд Тейлора в окрестности рабочей точки и ограничение числа членов разложения позволяет приближенно перейти к более простой степенной аппроксимации. Применение последней для решения спектральной задачи уже было изучено.

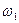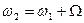Пример. При сложении двух синусоидальных колебаний близких частот (и , где 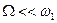) образуются биения. Их можно описать как АМ колебания с частотой заполнения 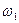и огибающей

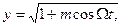(3.18)

где 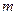- параметр, называемый глубиной модуляции.

Найдем спектр огибающей. Представим функцию (3.18) как 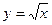, где 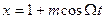. Разложим эту функцию в ряд Тейлора в окрестности единицы:

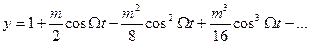(3.19)

Используя тригонометрические формулы

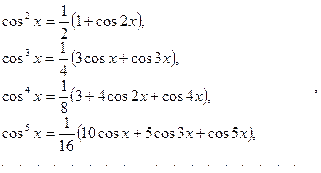
найдем спектр огибающей (3.18):

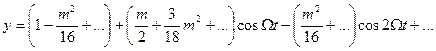(3.20)

Видно, что колебания огибающей не являются гармоническими. Однако, если амплитуды складываемых колебаний сильно различаются, то 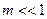. Тогда в линейном приближении имеем:

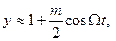(3.21)

и колебания огибающей приближенно оказываются гармоническими.

На рис. 3.5 методом проекций определен отклик нелинейного элемента, обладающего гистерезисом, на воздействие косинусоидального сигнала, например, - тока в случае индуктивного элемента. Пунктирная линия изображает первую гармонику 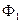магнитного потока. Использована кусочно-линейная аппроксимация ампервеберной характеристики элемента.

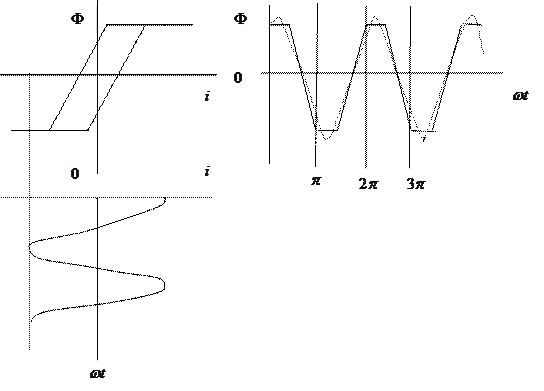Рис. 3.5

Первая гармоника магнитного потока 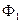сдвинута относительно входного сигнала 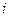по фазе на угол .

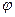Вывод: Наличие гистерезиса приводит к появлению сдвига фаз между воздействующим гармоническим сигналом и первой гармоникой негармонического отклика.