Интерполяция

Решение задачи интерполяции с помощью метода статистических испытаний рассмотрим на примере линейной интерполяции в многомерном кубе[1].

Пусть определена некоторая функция y = f (x ₁,…, x_n) в пространстве размерности n. Ее значения определены в вершинах e_i, i = 1,2,…,2 ⁿ единичного куба G (x ₁,…, x_n) = [0,1] ⁿ, где e_ij = 0,1; j = 1,2,…, n, т.е. компоненты векторов 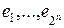могут принимать значения либо 0, либо 1. Задача состоит в нахождении путем линейной интерполяции значения функции f в произвольной точке (x ₁,…, x_n), лежащей внутри куба или на его границе.

Приведем формулы линейной интерполяции для одномерного и двумерного случаев:

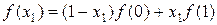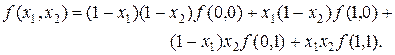(8)

Интерполяция функции в такой постановке становится проблемой в связи с тем, что количество слагаемых в интерполяционном выражении растет по закону 2 ⁿ и уже при n = 10 становится больше 10³. Чтобы разрешить данное затруднение, воспользуемся методом статистических испытаний, придерживаясь следующего сценария.

По определенному правилу разыграем процесс выбора вектора из набора 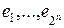, находим значение функции в данной точке, далее повторяем процедуру достаточное количество раз, находим среднее значение, которое и будет являться искомым интерполирующим значением. Итак, пусть задана произвольная точка (x ₁,…, x_n) Î G. Построим случайный вектор e = (e ₁,…, e_n), компоненты которого принимают значения 0 и 1 с вероятностями P (e_i = 0) = 1 - x_i, P (e_i = 1) = x_i, i = 1,…, n. Искомое интерполирующее значение будет найдено по формуле , где M — обозначает математическое ожидание или среднее значение функции в случайных вершинах единичного куба при повторных статистических испытаниях.

На листинге_№4 приведен пример решения задачи интерполяции методом Монте-Карло в двумерном случае. В данном случае задача линейной интерполяции осуществляется с помощью функции (8), которая и выступает в качестве аналитического решения.

Листинг_№4

%Программа моделирования линейной интерполяции в

%единичном квадрате G(x1,x2)=[0,1]x[0,1] с помощью

%метода Монте-Карло

function square

%Выбираем длину статистической серии для

%определения значения интерполирующей функции в

%некоторой точке внутри квадрата

N=1000;

%Определяем число узлов сетки по координатам x1 и x2

n1=21; n2=21;

%Определяем шаги сеток по координатам x1 и x2

h1=1.0/(n1-1); h2=1.0/(n2-1);

%Определяем сетки по координатам x1 и x2

x1=0:h1:1; x2=0:h2:1;

%Определяем значения интерполирующей функции (8) в

%узлах сетки

for i1=1:n1

for i2=1:n2

z(i1,i2)=f_interpl(x1(i1),x2(i2));

end

%Рисуем профиль точной интерполирующей функции (8)

subplot(1,2,1); surf(x2,x1,z);

%Организуем цикл расчета задачи интерполяции

%методом Монте-Карло в узлах сетки

for i1=1:n1

for i2=1:n2

s=0;

for n=1:N

e=rand(1,2)<=[x1(i1) x2(i2)];

s=s+f_vertex(e(1),e(2));

end

Monte_Carlo(i1,i2)=s/N;

end

%Рисуем результат моделирования задачи интерполяции

%методом Монте-Карло

subplot(1,2,2); surf(x2,x1,Monte_Carlo);

%Определение интерполируемой функции в узлах квадрата

function y=f_vertex(x1,x2)

y=(-1+x1+x2)^2;

%Аналитическая интерполирующая функция

function y=f_interpl(x1,x2)

y=(1-x1)*(1-x2)*f_vertex(0,0)+x1*(1-x2)*f_vertex(1,0)+...

(1-x1)*x2*f_vertex(0,1)+x1*x2*f_vertex(1,1);

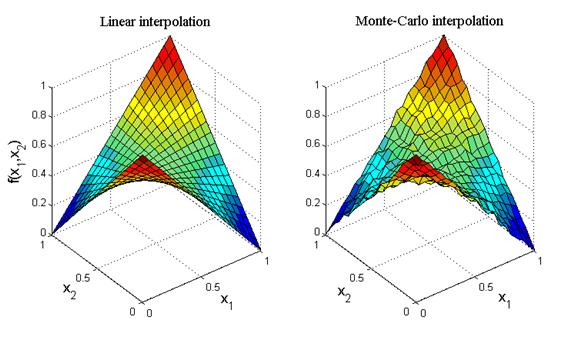
Рис.4. Решение задачи линейной интерполяции методом Монте-Карло в
единичном квадрате

На рис.4 приведен итог работы кода программы листинга_№4. На левой фигуре построен профиль интерполирующей функции (8), заданной в программе листинга_№4 своими значениями в вершинах единичного квадрата. На правой фигуре построен интерполирующий профиль, полученный методом Монте-Карло. Выбиралась скромная серия статистических испытаний в количестве 10³ в расчете на определение значения интерполирующей функции в одной точке.

На листинге_№5 приведен код программы интерполирования функции, заданной в вершинах многомерного куба (n = 100).

Листинг_№5

%Программа интерполяции в многомерном кубе

%функции, заданной в вершинах куба

function cube

%Определяем размерность куба

n=100;

%Определяем точку, в которую функция

%будет интерполирована

x=0.5*ones(1,n);

k=0;

%Организуем цикл статистических испытаний с

%различной длиной статистических серий

for N=2000:2000:100000

s=0; sd=0;

for i=1:N

e=rand(1,n)<=x;

fv=f_vertex(e);

s=s+fv; sd=sd+fv^2;

end

k=k+1;

%Вычисляем среднее Mf(e1,...,en) значение

%интерполируемой функции в выбранной точке x

Mf(k)=s/N;

%Определяем дисперсию Df(e1,...,en)

%интерполируемой функции в выбранной точке x

Df(k)=sd/N-Mf(k)^2;

lng(k)=N;

end

%Рисуем зависимость среднего значения интерполируемой

%функции от длины статистической серии N

subplot(1,2,1); semilogx(lng,Mf);

%Рисуем зависимость дисперсии интерполируемой

%функции от длины статистической серии N

subplot(1,2,2); semilogx(lng,Df);

%Определение интерполируемой функции в узлах

%многомерного куба

function y=f_vertex(e)

y=sum(e);

На рис.5 приведен итог работы кода программы листинга_№5. Решалась задача интерполирования методом Монте-Карло функции, заданной в вершинах 100-мерного куба. На левой фигуре изображено значение интерполирующей функции в точке (0.5,…,0.5) в зависимости от длины статистической серии. Видно, что колебания происходят вокруг значения 50 со средней амплитудой 0.05 при максимальной длине статистической серии 10⁵. На правой фигуре изображена дисперсия интерполирующей функции в зависимости от длины статистической серии.