Лекция №15
Метод статистических испытаний
(метод Монте-Карло)
Метод статистических испытаний или метод Монте-Карло занимается использованием случайных чисел для решения различных математических задач: интерполяции, вычисления интегралов, решение дифференциальных и интегральных уравнений, решения систем линейных уравнений, поиска экстремумов, моделирования тех или иных процессов и для решения многих других задач. Преимущество метода Монте-Карло, в котором используются недетерминированные процедуры, особенно ярко проявляются при решении задач большой размерности, когда использование обычных детерминированных методов затруднительно или вовсе невозможно. По мере развития вычислительной техники граница между возможным и невозможным сдвигается в сторону невозможности, но всегда остается. Основным недостатком метода Монте-Карло является его медленная сходимость, что вынуждает учитывать баланс между точностью результатов и затратами машинного времени.
Величину x называют случайной с плотностью распределения r (x), если вероятность того, что величина примет значение между x 1 и x 2 равна 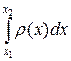 . В силу определения вероятности, r (x) неотрицательна и нормирована на единицу, т.е.
. В силу определения вероятности, r (x) неотрицательна и нормирована на единицу, т.е.
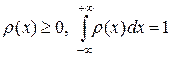 . (1)
. (1)
Если значения x всегда заключены между a и b, то r (x) = 0 вне данных пределов. В этом случае интеграл в (1) следует брать по отрезку [ a, b ].
Случайная величина x может быть дискретной, т.е. принимать только вполне определенные значения xi с вероятностью ri. Дискретную величину можно формально объединить с непрерывной, считая
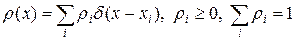 ,
,
где 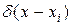 — дельта-функция.
— дельта-функция.
Если по значениям случайной величины x вычисляют какую-либо функцию f (x), то значения данной функции также будут случайными. Данную функцию иногда называют случайной.
Равномерно распределенная величина. Рассмотрим случайную функцию
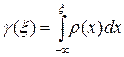 , (2)
, (2)
которая принимает значения из отрезка [0,1] и монотонно зависит от x. Вероятность того, что g лежит между g 1 = g (x 1) и g 2 = g (x 2), равна вероятности того, что x лежит между x 1 и x 2. Вероятность того, что x Î [ x 1, x 2] равна согласно (2) 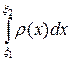 = g 2 - g 1, т.е. эта вероятность равна длине отрезка [ g 1, g 2] и не зависит от положения отрезка. Другими словами, величина g (x) принимает с равной вероятностью любые значения из отрезка [0,1]. Плотность распределения такой случайной величины g равна
= g 2 - g 1, т.е. эта вероятность равна длине отрезка [ g 1, g 2] и не зависит от положения отрезка. Другими словами, величина g (x) принимает с равной вероятностью любые значения из отрезка [0,1]. Плотность распределения такой случайной величины g равна
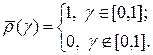
 2014-02-09
2014-02-09 653
653








