Некорректные задачи

Регуляризация. Если правая часть нелинейного интегрального уравнения не зависит от решения, которое, таким образов, входит лишь под знак интеграла, то задача оказывается некорректно поставленной.

Классическими примерами некорректных задач являются уравнение Фредгольма первого рода

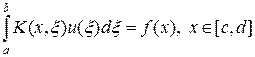(35)

и уравнение Вольтерра первого рода

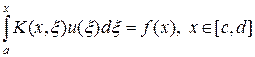. (36)

В отличие от уравнений Фредгольма и Вольтерра второго рода, ядро уравнения первого рода (35) определено на прямоугольнике (x, x) Î [ c, d ]´[ a, b ], а ядро уравнения (36) — на трапеции (x, x) Î [ c, d ]´[ a, x ] при c < a или на двух треугольниках при c > a. При этом функции u (x) и f (x) определены на разных отрезках и принадлежат разным классам функций.

Покажем, что уравнение Фредгольма первого рода (35) неустойчиво по правой части и, тем самым, является некорректным. Рассмотрим возмущение решения du (x) специального вида, а именно du (x) = exp(iwx). Данному возмущению соответствует возмущение правой части вида:

.

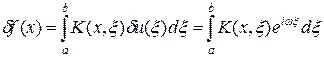Интегрируя последний интеграл по частям, находим

,

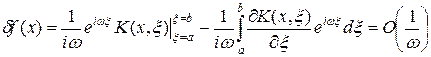т.е. для достаточно больших частот | w | >> 1 величина 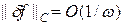может быть как угодно малой. Таким образом, существуют такие сколь угодно малые возмущения правой части df (x), которым соответствуют большие возмущения решения du (x), т.е. уравнение Фредгольма первого рода (35) является некорректным. Для уравнения Вольтерра (36) справедливы те же рассуждения относительно устойчивости по правой части.

Отметим, что с некорректной задачей мы уже сталкивались, осуществляя численное дифференцирование в лекции №3. Действительно численное дифференцирование некоторой функции f (x) сводится к решению уравнения

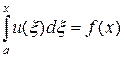, (37)

которое является частным случаем уравнения Вольтерра первого рода с ядром K (x, x) = 1 при x £ x.

Задачи (35), (36) имеют решения не при любых непрерывных правых частях. Например, задача (37) имеет решение только для дифференцируемых правых частей 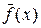. Другой пример дает уравнение (35), когда ядро является вырожденным типа (27). В этом случае правая часть f (x) должна быть представима в виде:

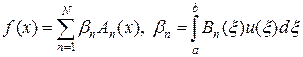. (38)

Таким образом, согласно (38), уравнение (35) имеет решения лишь для таких правых частей 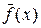, которые представимы в виде (38). Для других правых частей решение задачи (35) не существует.

Приведенные выше два примера говорят о том, что даже если решения задач (35), (36) и существуют при некоторых правых частях 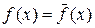, всегда найдутся такие возмущения df (x) правых частей, при которых решения не существуют. Из этого ясно, что решать некорректные задачи при неточно заданных правых частях бессмысленно. Если правая часть 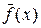задана с погрешностью df (x), то соответствующее решение 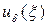либо не существует, либо отличается от искомого решения 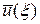на величину 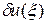, которая может быть большой. Даже в том случае, когда правая часть задана точно, а решение находится одним из численных методов, неизбежны ошибки округления, что может привести к большой погрешности решения.

Определим регуляризирующий алгоритм. Пусть требуется найти решение u (x) некорректной задачи:

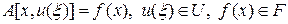, (39)

где A — некоторый оператор,, U и F — нормированные пространства. Предполагается, что для произвольной правой части f (x) Î F решение задачи (39) может не существовать. Однако могут существовать некоторые правые части 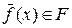, для которых существует решение .

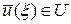Наряду с задачей (39), рассмотрим задачу

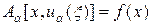, (40)

в которую введен дополнительный член с малым положительным параметром регуляризации a.

Определение. Оператор A_a называют регуляризирующим, если 1) задача (40) является корректно поставленной в классе правых частей F при любом (не слишком большом) a > 0 и 2) для любого e > 0 существуют такие функции a (d) и d (e), что если 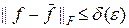, то .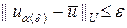

Отметим, что выбор функций a (d) и d (e) зависит, в том числе и от 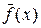. Итак, если найден регуляризирующий оператор A_a, то задача (40) имеет решение для любых правых частей f (x) Î F, в том числе и для тех, которые отличаются от 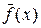на любую величину погрешности df (x), т.е. задача является устойчивой и корректной и она может быть решена обычными вычислительными методами. При правильно подобранном значении параметра a решение задачи (40) 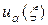будет мало отличаться от интересующего нас решения 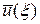задачи (39).

Различают регуляризацию слабую, сильную и p -го порядка гладкости в зависимости от того является ли пространство U гильбертовым, чебышевским или пространством C ^{( p )}© соответственно.

Вариационный метод регуляризации состоит в сведении исходной задачи (35) к вариационной задаче:

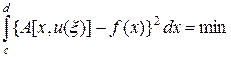, (41)

где

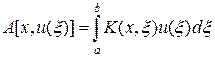. (42)

Рассмотрим модифицированную задачу (41) согласно формуле:

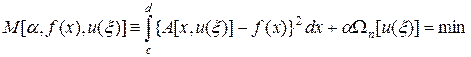, (41¢)

где определен так называемый тихоновский стабилизатор n -го порядка W _n, имеющий следующий вид:

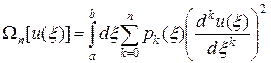. (42)

В (42) весовые функции p_k (x) считаются непрерывными и положительными, а если нет специальных условий для их определения, то они полагаются единичными.

Если ввести на множестве функций U норму 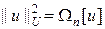, то данное пространство называют пространством Соболева 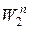. Множество правых частей будем считать гильбертовым пространством. Покажем, что задача (41¢) является регуляризирующей для решения некорректной задачи (35).

Теорема №1. Задача (41¢) имеет решение u_a (x) при любых f (x) и a > 0.

Доказательство. При a > 0 функционал 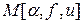ограничен снизу и при заданных a и f (x) имеет точную нижнюю грань. Выберем некоторую минимизирующую последовательность u_i (x), i = 0,1,2,… так, чтобы последовательность 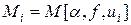не возрастала, при этом

,

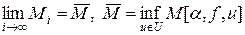тогда

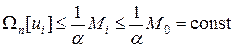. (43)

Согласно (43), последовательность u_i (x), i = 0,1,2,… принадлежит множеству функций u (x), которые определяются условием 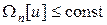. Последнее множество является компактом в U. Поэтому из последовательности u_i (x), i = 0,1,2,… можно выделить подпоследовательность 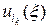, k = 0,1,2,…, которая сходится по норме к некоторой 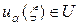. В силу непрерывности функционал 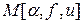на функции 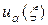достигает свой нижней грани, т.е. функция 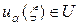является решением задачи (41¢), (42). Доказательство завершено.

Теорема №2. Задача (41¢), (42) является регуляризирующей для задачи (41).

Доказательство. Введем обозначения: пусть 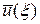— решение исходной задачи (41), 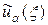— решение модифицированной задачи (41¢) с приближенной правой частью 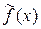. Определим также функцию .

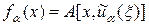Поскольку функционал 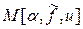достигает минимума на 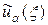, постольку 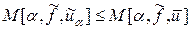. Учитывая последнее неравенство и определение функционала (41¢), получим

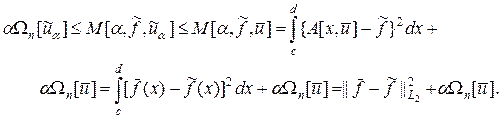(44)

Пусть приближенная правая 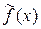часть удовлетворяет условию

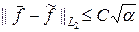, (45)

где C = const. Подставляя (45) в (44), находим

,

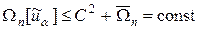где 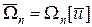. Таким образом, решение регуляризированной задачи 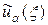принадлежит компактному множеству U ₀ функций из U. Тому же множеству U ₀ принадлежит и решение исходной задачи .

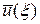Пусть F ₀ — множество функций 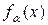, которые являются образом множества U ₀ при отображении A, т.е. A: U ₀ ® F ₀. Будем предполагать, что интегральный оператор A непрерывен и обратное отображение единственно. При этих условиях обратное отображение F ₀ в компактное множество U ₀ при помощи оператора A ^-1 непрерывно в 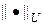. Таким образом, для произвольного e > 0 найдется такое b (e), что если 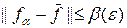, то .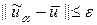

Учитывая (44), получим

.

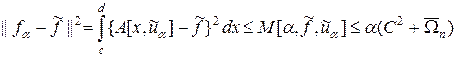С учетом последнего неравенства и неравенства (45), найдем

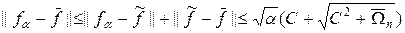. (46)

Выберем параметр a так, чтобы выполнялось неравенство

a £ a ₀(e), (47)

где 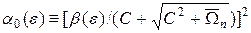. В этом случае правая часть неравенства (46) будет меньше b (e), откуда следует, что .

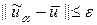Таким образом, по заданному e нашлось такое a ₀(e) и такое 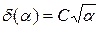, что если a £ a ₀(e) и 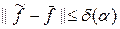, то 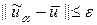, что и требовалось доказать.

Следствие. Задача (41¢), (42) корректно поставлена.

Подставим в теорему №2 всюду вместо оператора A регуляризованный оператор, соответствующий решению задачи (41¢), (42). В этом случае малость 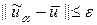означает, что регуляризованное решение 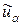непрерывно зависит от правой части .

Выбор параметра a состоит в поиске среднего значения между слишком малым и слишком большим значениями. В ряде прикладных задач известно, что правая часть имеет характерную погрешность 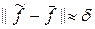. Если в этом случае выбрать параметр a настолько малым, что нарушится условие (45), то устойчивость расчета может оказаться недостаточной и регуляризованное решение 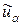будет заметно “разболтанным”. Если же параметр a настолько велик, что нарушается критерий (47), то регуляризованное решение 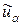будет чрезмерно сглаженным. На практике проводят расчеты с несколькими значениями параметра a. Из полученных результатов выбирают наилучший согласно какому-нибудь правдоподобному критерию.

Выбор n. При чрезмерно большом n регуляризованное решение сильно сглаживается. Значение n = 0 обеспечивает среднеквадратическую сходимость 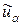к 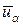. По этой причине наиболее часто используют n = 1.

Уравнение Эйлера. Перепишем задачу (41¢), (42) в развернутом виде:

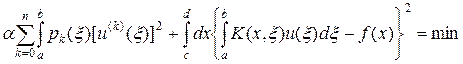. (48)

Составим для задачи (48) уравнения Эйлера путем приравнивания к нулю вариации левой части по u (x):

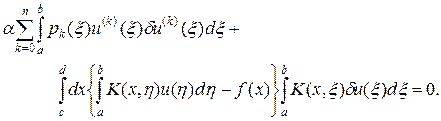(49)

Интегралы, стоящие под знаком суммы в (49), вычислим последовательным интегрированием по частям:

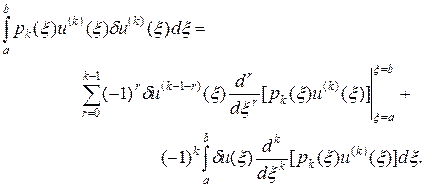(50)

Подставляя (50) в (49) и меняя порядок суммирования в двойной сумме, найдем

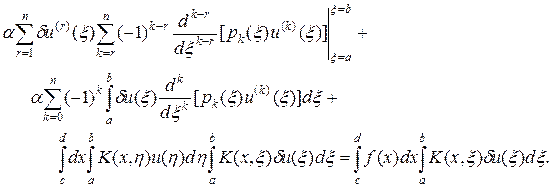
Приравнивая в этом выражении коэффициенты при вариации du (x) к нулю, найдем искомое интегро-дифференциальное уравнение Эйлера

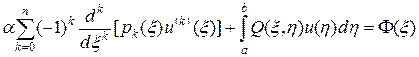, (51)

с ядром и правой часть

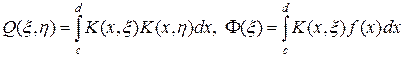(51¢)

и краевыми условиями

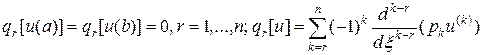. (51¢¢)

Отметим, что ядро Q (x, h) определено в квадрате [ a, b ]´[ a, b ] симметрично и непрерывно, а правая часть F(x) непрерывна.

Докажем, что задача (41¢), (42) в форме уравнения Эйлера (51) является регуляризирующим алгоритмом.

Теорема №1. Задача (51) — (51¢¢) корректно поставлена при любом a > 0.

Доказательство. В начале рассмотрим простейший случай n = 0. Тогда производные неизвестной функции в уравнении (51) и граничные условия (51¢¢) исчезнут и уравнение (51) превратиться в интегральное уравнение Фредгольма второго рода:

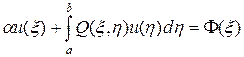(52)

с ядром и правой частью (51¢).

Обозначим через l_i, u_i (x) — i -ое собственное значение и собственную функцию ядра Q (x, h). В силу определения ядра в (51¢) имеем

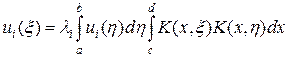. (53)

Умножая уравнение (53) на u_i (x) и интегрируя, найдем

,

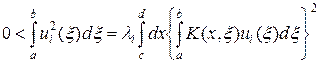т.е. все собственные значения ядра Q (x, h) положительны. По этой причине и согласно теории интегральных уравнений Фредгольма, при любом a > 0 уравнение (52) имеет решение u_a (x), которое единственно и непрерывно зависит от правой части F(x) и, тем самым, от f (x). В итоге, при n = 0 задача (52) и эквивалентная ей задача (41¢) корректны.

При n > 0 задачу (51) — (51¢¢) также можно свести к интегральному уравнению Фредгольма второго рода, ядро которого имеет положительные собственные значения. Чтобы это увидеть, построим функцию Грина G (x, t) для дифференциального оператора, стоящего в левой части (51), при учете краевых условий (51¢¢). Рассматривая все остальные члены уравнения (51) как правую часть и используя функцию Грина, найдем

.

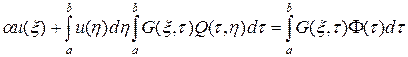Таким образом, задача (51) — (51¢¢) корректна при любом n, когда a > 0, что и требовалось доказать.

Рассмотрим пример решения уравнения Фредгольма первого рода

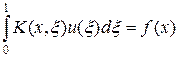(54)

в квадрате (x, x) Î [0,1]´[0,1] с ядром и правой частью вида:

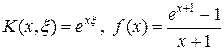. (54¢)

Задача (54), (54¢) имеет аналитическое решение 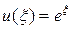. Задачу (54), (54¢) решим методом регуляризации при n = 0, т.е. путем решения интегрального уравнения Фредгольма второго рода (53) с ядром и правой частью, определенных в (51¢). Учитывая (51¢), (52), (54¢), решение задачи (54), (54¢) сведем к решению уравнения Фредгольма второго рода:

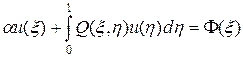, (55)

где

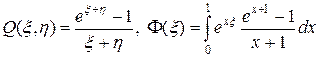. (55¢)

Для численного решения уравнения (55) введем равномерные сетки по переменным x и h: x_i = h (i - 1), h_j = h (j - 1), h = 1/(N - 1), i, j = 1,2,…, N. Интеграл, входящий в уравнение (55), аппроксимируем по формуле трапеции, тогда получим следующую разностную схему:

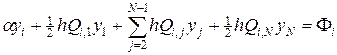, (56)

где 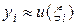, , 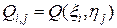, 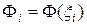i, j = 1,2,…, N.

На листинге_№7 приведен код программы решения задачи (54), (54¢) методом регуляризации, т.е. путем сведения исходной задачи к решению уравнения Фредгольма второго рода (55) с параметром регуляризации a > 0.

Листинг_№7

%Пример решения некорректного уравнения Фредгольма

%первого рода (54) с помощью метода регуляризации,

%т.е. путем сведения исходной задачи (54), (54') к

%решению корректного уравнения Фредгольма второго

%рода (55) с параметром регуляризации alpha > 0

function noncor

%Вводим число узлов сетки по переменным xi и eta

N=101; h=1.0/(N-1);

xi=0:h:1; eta=0:h:1;

%Определяем значения аналитического решения exp(xi)

%в узлах сетки xi

ya=exp(xi);

%Рисуем аналитическое решение пунктирной

%красной линией

subplot(1,2,1);

plot(xi,ya,'--','Color','red','LineWidth',4.5);

hold on

%Определяем набор параметров регуляризации alpha

alpha=[1e-2 1e-3 3e-4 1e-4 5e-5 1e-5];

%Организуем цикл расчетов с различными значениями

%параметра регуляризации

for s=1:length(alpha)

%Согласно разностной схеме (56) определяем

%линейную систему уравнений Ay = b относительно

%неизвестного вектора y

for i=1:N

A(i,1)=0.5*h*Q(xi(i),eta(1));

A(i,N)=0.5*h*Q(xi(i),eta(N));

for j=2:(N-1)

A(i,j)=h*Q(xi(i),eta(j));

end

A(i,i)=A(i,i)+alpha(s);

b(i)=f(xi(i));

end

%Решаем линейную систему уравнений Ay = b

y=A\b';

%Оцениваем ошибку численного решения y путем

%оценки разности error=||y-ya|| в норме C, где

%ya - аналитическое решение задачи (54), (54')

for i=1:N

z(i)=abs(y(i)-ya(i));

end

error(s)=max(z);

%Рисуем регуляризированные решения y при

%различных значениях параметра alpha

subplot(1,2,1); plot(xi,y,'LineWidth',3.5/s);

hold on

end

%Рисуем график зависимости ошибки численного

%решения от параметра alpha

subplot(1,2,2); loglog(alpha,error,'LineWidth',3);

%Определяем функцию Q(xi,eta), заданную в (55')

function y=Q(xi,eta)

if (xi==0)&(eta==0)

y=1;

else

y=(exp(xi+eta)-1)/(xi+eta);

end

%Определяем функцию f(xi), заданную в (55')

function y=f(xi)

%Используем формулу трапеции для аппроксимации

%интеграла, входящего в определение f(xi) в (55')

y=0.005*(fi(0,xi)+fi(1,xi));

for i=2:100

y=y+0.01*fi(0.01*(i-1),xi);

end

function y=fi(x,xi)

y=exp(x*xi)*((exp(x+1)-1)/(x+1));

На рис.7 приведен итоговый график, генерируемый кодом программы листинга_№7. На левом рисунке приведены графики численного решения 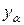при различных значениях регуляризирующего значения. Видно, что как слишком большие значения, так и слишком малые значения приводят к большим отличиям от аналитического решения 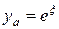. Аналитическое решение 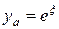представлено на левом рисунке в виде красной жирной пунктирной линии. На правом рисунке представлена зависимость ошибки численного решения error = 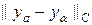от параметра регуляризации a > 0. Из правого графика отчетливо видно наличие оптимального значения параметра a _opt регуляризации, при котором ошибка достигает минимума. В программе следующего листинга_№8 будет изучена зависимость оптимального значения параметра регуляризации a _opt от шага сетки h.

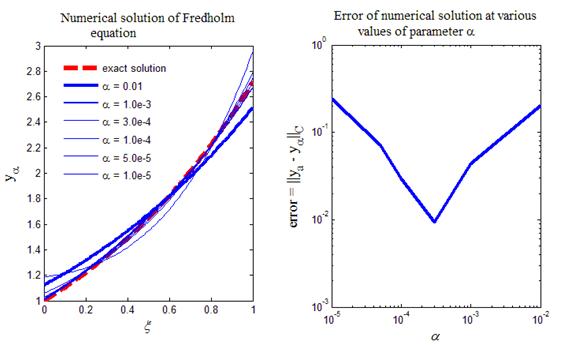
Рис.7. Численное решение некорректной задачи (54), (54¢) методом
регуляризации, т.е. путем сведения ее к решению корректного
уравнения Фредгольма второго рода (55)

На листинге_№8 приведено решение предыдущей некорректной задачи (54), (54¢) методом регуляризации с помощью решения корректного уравнения Фредгольма второго рода (55), (55¢). В этой программе нас будет интересовать зависимость оптимального значения параметра a _opt от шага сетки h. Напомним, что сетки были введены по переменным x и h для аппроксимации интеграла в интегральном уравнении (55) согласно разностной схеме (56). Необходимо убедиться, что при уменьшении шага сетки a _opt также уменьшается.

Листинг_№8

%На примере решения некорректного уравнения Фредгольма

%первого рода (54) с помощью метода регуляризации,

%т.е. путем сведения исходной задачи (54), (54') к

%решению корректного уравнения Фредгольма второго

%рода (55) исследуется зависимость оптимального

%значения параметра alpha_opt от шага сетки h

function noncor2

global N h

%Вводим начальное число узлов сетки по

%переменным xi и eta

N=21;

%Организуем цикл расчетов с разным сетками

for t=1:6

%Число узлов сетки по переменным xi и eta

%увеличиваем в арифметической прогрессии

N=N+20; h=1.0/(N-1);

xi=0:h:1; eta=0:h:1;

%Определяем значения аналитического решения exp(xi)

%в узлах сетки xi

ya=exp(xi);

%Определяем набор параметров регуляризации alpha

alph_l=1e-4; alph_r=1e-3; alph_h=(alph_r-alph_l)/20;

alpha=alph_l:alph_h:alph_r;

%Организуем цикл расчетов с различными значениями

%параметра регуляризации

for s=1:length(alpha)

%Согласно разностной схеме (56) определяем

%линейную систему уравнений Ay = b относительно

%неизвестного вектора y

for i=1:N

A(i,1)=0.5*h*Q(xi(i),eta(1));

A(i,N)=0.5*h*Q(xi(i),eta(N));

for j=2:(N-1)

A(i,j)=h*Q(xi(i),eta(j));

end

A(i,i)=A(i,i)+alpha(s);

b(i)=f(xi(i));

end

%Решаем линейную систему уравнений Ay = b

y=A\b';

%Оцениваем ошибку численного решения y путем

%оценки разности error=||y-ya|| в норме C, где

%ya - аналитическое решение задачи (54), (54')

for i=1:N

z(i)=abs(y(i)-ya(i));

end

error(s)=max(z);

end

%Определяем значение alph_opt, при котором ошибка

%численного решения минимальна

ermin=min(error);

for s=1:length(alpha)

if ermin==error(s)

alph_opt(t)=alpha(s);

end

end

step(t)=h;

%Рисуем график зависимости ошибки численного

%решения от параметра alpha

subplot(1,2,1);

loglog(alpha,error,'LineWidth',0.75*t);

hold on

end

%Рисуем график зависимости оптимального значения

%параметра регуляризации alph_opt от шага сетки

subplot(1,2,2); plot(step,alph_opt);

%Определяем функцию Q(xi,eta), заданную в (55')

function y=Q(xi,eta)

if (xi==0)&(eta==0)

y=1;

else

y=(exp(xi+eta)-1)/(xi+eta);

end

%Определяем функцию f(xi), заданную в (55')

function y=f(xi)

global N h

%Используем формулу трапеции для аппроксимации

%интеграла, входящего в определение f(xi) в (55')

y=0.5*h*(fi(0,xi)+fi(1,xi));

for i=2:(N-1)

y=y+h*fi(h*(i-1),xi);

end

function y=fi(x,xi)

y=exp(x*xi)*((exp(x+1)-1)/(x+1));

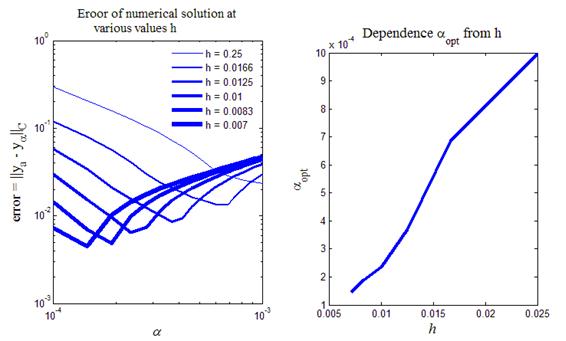
Рис.8. Изучение зависимости оптимального значения параметра
регуляризации a _opt от шага сетки h

На рис.8 приведен итог работы кода программы листинга_№8. На левом рисунке приведены графики зависимости ошибки численного решения в зависимости от значений регуляризирующего параметра a, полученные на различных сетках, т.е. при разных шагах h по переменным x и h. На всех шести графиках отмечается наличие оптимального значения параметра регуляризации a _opt. На правом графике построен профиль зависимости a _opt от шага сетки h. Видно, что оптимальное значение параметра регуляризации стремится к нулю по мере стремления шага сетки к нулю.

Можно доказать еще ряд важных утверждений при n = 1. Во-первых, решение регуляризованное задачи (51) — (51¢¢) равномерно сходится к решению исходной задачи (39), во-вторых, метод регуляризации при n = 1 обеспечивает сильную регуляризацию. Приведем лишь формулировки соответствующих теорем, опуская доказательства (формулировки и доказательства данных теорем приведены в учебнике[5]).

Теорема №2. Пусть 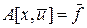, тогда при n = 1 и положительном a ® 0 решение 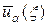задачи (51) — (51¢¢), соответствующее правой части 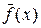, равномерно сходится к .

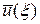Теорема №3. Метод регуляризации (41¢), (42) при n = 1 обеспечивает сильную регуляризацию, т.е. регуляризованное решение сходится к искомому решению в норме .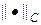

Более подробно рассмотрим случай n = 1 на примере решения задачи (54) с ядром и правой частью вида:

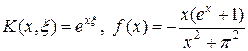. (57)

Задаче (54), (57) соответствует аналитическое решение u (x) = cos(px).

Согласно (51), (51¢¢), имеем (p ₀(x) º 1, p ₁(x) º 1):

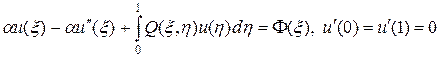, (58)

где функции Q (x, h), F(x) с учетом (51¢), (57) имеют следующий вид:

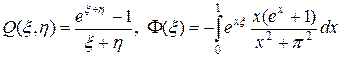. (58¢)

Для решения задачи (58), (58¢) введем сетки по переменным x и h: x_i = h (i - 1), h_j = h (j - 1), h = 1/(N - 1), i, j = 1,2,…, N. Интеграл, входящий в (58), аппроксимируем по формуле трапеции, тогда

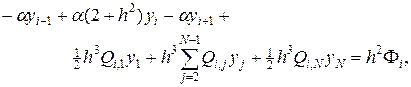(59)

где y_i» u (x_i), i = 2,…, N. Недостающие два уравнения находятся из граничных условий, которые аппроксимируем со вторым порядком по h, т.е.

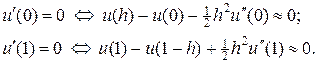(60)

Находя соответствующие 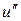из уравнения (58) и подставляя в (60), получим граничные условия в следующем виде:

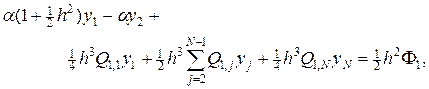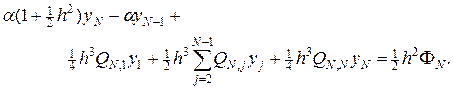(61)

(61¢)

На листинге_№9 приведен код программы решения некорректной задачи (54), (57) методом регуляризации, т.е. путем сведения исходной задачи к решению корректного интегро-дифференциального уравнения (58), (58¢). Как и в предыдущих двух программах, выбор параметра регуляризации a определяется его оптимальным значением a _opt, на котором реализуется минимум ошибки численного решения (при условии, конечно, что решение известно). В программе листинга_№9 исследуется зависимость оптимального значения параметра регуляризации a _opt от шага сетки h.

Листинг_№9

%На примере решения некорректного уравнения Фредгольма

%первого рода (54) с помощью метода регуляризации,

%т.е. путем сведения исходной задачи (54), (57) к

%решению корректного интегро-дифференциального уравнения

%(58), (58') исследуется зависимость оптимального

%значения параметра alpha_opt от шага сетки h

function noncor3

global N h

%Вводим начальное число узлов сетки по

%переменным xi и eta

N=21;

%Организуем цикл расчетов с разным сетками

for t=1:5

%Число узлов сетки по переменным xi и eta

%увеличиваем в арифметической прогрессии

N=N+30; h=1.0/(N-1); h2=h^2; h3=h^3;

xi=0:h:1; eta=0:h:1;

%Определяем значения аналитического решения cos(pi*xi)

%в узлах сетки xi

ya=cos(pi*xi);

%Определяем набор параметров регуляризации alpha

alph_l=7e-6; alph_r=2e-5; alph_h=(alph_r-alph_l)/20;

alpha=alph_l:alph_h:alph_r;

%Организуем цикл расчетов с различными значениями

%параметра регуляризации

for s=1:length(alpha)

%Согласно разностной схеме (59), (61), (61')

%определяем линейную систему уравнений Ay = b

%относительно неизвестного вектора y

%Определяем левое граничное условие согласно (61)

A(1,1)=0.25*h3*Q(xi(1),eta(1));

A(1,N)=0.25*h3*Q(xi(1),eta(N));

for j=2:(N-1)

A(1,j)=0.5*h3*Q(xi(1),eta(j));

end

A(1,1)=A(1,1)+alpha(s)*(1+0.5*h2);

A(1,2)=A(1,2)-alpha(s);

b(1)=0.5*h2*f(xi(1));

%Определяем элементы матрицы A согласно (59)

for i=2:(N-1)

A(i,1)=0.5*h3*Q(xi(i),eta(1));

A(i,N)=0.5*h3*Q(xi(i),eta(N));

for j=2:(N-1)

A(i,j)=h3*Q(xi(i),eta(j));

end

A(i,i)=A(i,i)+alpha(s)*(2+h2);

A(i,i-1)=A(i,i-1)-alpha(s);

A(i,i+1)=A(i,i+1)-alpha(s);

b(i)=h2*f(xi(i));

end

%Определяем правое граничное условие (61')

A(N,1)=0.25*h3*Q(xi(N),eta(1));

A(N,N)=0.25*h3*Q(xi(N),eta(N));

for j=2:(N-1)

A(N,j)=0.5*h3*Q(xi(N),eta(j));

end

A(N,N)=A(N,N)+alpha(s)*(1+0.5*h2);

A(N,N-1)=A(N,N-1)-alpha(s);

b(N)=0.5*h2*f(xi(N));

%Решаем линейную систему уравнений Ay = b

y=A\b';

%Оцениваем ошибку численного решения y путем

%оценки разности error=||y-ya|| в норме C, где

%ya - аналитическое решение задачи (54), (57)

for i=1:N

z(i)=abs(y(i)-ya(i));

end

error(s)=max(z);

end

%Определяем значение alph_opt, при котором ошибка

%численного решения минимальна

ermin=min(error);

for s=1:length(alpha)

if ermin==error(s)

alph_opt(t)=alpha(s);

end

end

step(t)=h;

%Рисуем график зависимости ошибки численного

%решения от параметра alpha

subplot(1,2,1);

semilogx(alpha,error,'LineWidth',0.75*t);

hold on

end

%Рисуем график зависимости оптимального значения

%параметра регуляризации alph_opt от шага сетки

subplot(1,2,2); plot(step,alph_opt);

%Определяем функцию Q(xi,eta), заданную в (58')

function y=Q(xi,eta)

if (xi==0)&(eta==0)

y=1;

else

y=(exp(xi+eta)-1)/(xi+eta);

end

%Определяем функцию f(xi), заданную в (58')

function y=f(xi)

global N h

%Используем формулу трапеции для аппроксимации

%интеграла, входящего в определение f(xi) в (58')

y=0.5*h*(fi(0,xi)+fi(1,xi));

for i=2:(N-1)

y=y+h*fi(h*(i-1),xi);

end

function y=fi(x,xi)

y=-exp(x*xi)*((x*(exp(x)+1))/(x^2+pi^2));

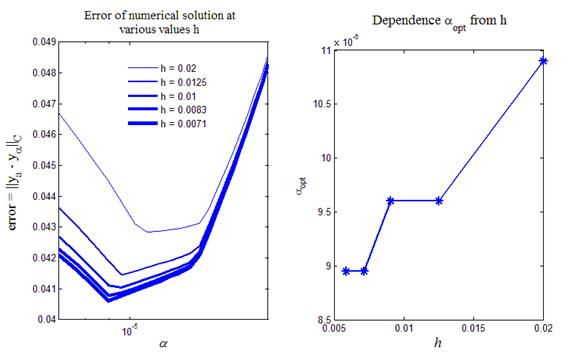
Рис.9. Изучение зависимости оптимального значения параметра
регуляризации a _opt от шага сетки h

На рис.9 приведен итог работы кода программы листинга_№9. На левом рисунке приведены пять графиков зависимости ошибки численного решения от параметра регуляризации a при различных значениях шага сетки h. На всех пяти графиках отчетливо видно наличие оптимального значения параметра регуляризации a _opt, при котором ошибка численного решения error = 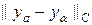(y_a = cos(px) — аналитическое решение исходной задачи (54), (57)) достигает минимального значения. На правом рисунке показана зависимость оптимального значения параметра регуляризации от шага сетки. Правый рисунок демонстрирует тенденцию стремления a _opt к нулю при h ® 0, что иллюстрирует сходимость регуляризированного решения y_a к аналитическому решению y_a исходной задачи.

Некоторые приложения метода регуляризации. Некорректно поставленные задачи встречаются в практике довольно часто. Это, например, сглаживание и дифференцирование экспериментально измеренных функций, суммирование рядов Фурье с неточно заданными коэффициентами, решение линейных плохо обусловленных систем уравнений, решение задач оптимального управления, аналитическое продолжение функций, обратные задачи теплопроводности и геологической разведки, восстановление переданного сигнала и многие другие задачи.

Сглаживание функции. Пусть функция f (x), x Î [ a, b ] измерена экспериментально и содержит заметную случайную ошибку. В терминах задачи (39) задача сглаживания функции f (x) состоит в решении некорректного уравнения 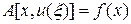, где 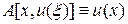. Применим метод регуляризации к данной задаче, ограничившись случаем n = 1, т.е. сильной регуляризацией. Тогда, принимая во внимание формулы (51) — (51¢¢), получим следующее уравнение Эйлера:

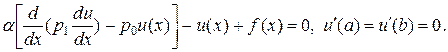(62)

Согласно (62), сглаженная функция u (x) удовлетворяет линейному дифференциальному уравнению второго порядка, для которого поставлена вторая краевая задача.

Для решения уравнения (62) введем сетку по переменной x: x_i = a + (i - 1) h, i = 1,…, N, h = (b - a)/(N - 1) и составим разностную схему:

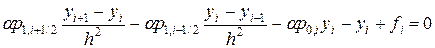, (63)

где y_i» u (x_i), 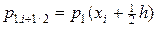, i = 2,…, N - 1. Недостающая пара уравнений вытекает из аппроксимации граничных условий со вторым порядком точности по шагу сетки:

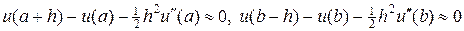. (64)

Находя значения 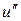в точках x = a и x = b из уравнения (62) и подставляя их в (64), получим следующие разностные уравнения для граничных условий:

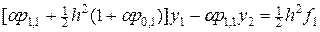, (65)

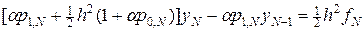. (65¢)

На листинге_№10 приведен код программы сглаживания функции f (x) с помощью метода сильной регуляризации, который сводится к решению обыкновенного дифференциального уравнения второго порядка (62) согласно разностной схеме (63), (65), (65¢).

Листинг_№10

%Программа сглаживания функции с помощью метода

%сильной регуляризации путем решения дифференциального

%уравнения второго порядка (62) согласно разностным

%схемам (63), (65), (65')

function smoothing

%Определяем область интегрирования

a=0; b=1;

%Определяем число узлов разностной схемы и ее шаг

N=101; h=(b-a)/(N-1);

%Определяем сетку по x

x=a:h:b;

%Определяем функцию, которая немного зашумлена

for i=1:N

f(i)=x(i)*sin(2*pi*x(i))+0.1*randn;

end

%Выбираем пару значений параметра регуляризации

alpha=[1e-3 1e-4];

%Организуем цикл расчетов с разными значениями

%параметра регуляризации

for s=1:length(alpha)

%Вычисляем начальные значения коэффициентов

%прогонки y(i-1)=c(i)y(i)+d(i), учитывая левое

%граничное условие (65)

c(2)=(alpha(s)*p1(x(1)))/...

(alpha(s)*p1(x(1))+0.5*h^2*(1+alpha(s)*p0(x(1))));

d(2)=(0.5*h^2*f(1))/...

(alpha(s)*p1(x(1))+0.5*h^2*(1+alpha(s)*p0(x(1))));

%Вычисляем коэффициенты прогонки

for i=2:(N-1)

c(i+1)=(alpha(s)*p1(x(i)+0.5*h))/...

(h^2*(1+alpha(s)*p0(x(i)))+alpha(s)*...

(p1(x(i)+0.5*h)+p1(x(i)-0.5*h))-...

alpha(s)*p1(x(i)-0.5*h)*c(i));

d(i+1)=(alpha(s)*p1(x(i)-0.5*h)*d(i)+h^2*f(i))/...

(h^2*(1+alpha(s)*p0(x(i)))+alpha(s)*...

(p1(x(i)+0.5*h)+p1(x(i)-0.5*h))-...

alpha(s)*p1(x(i)-0.5*h)*c(i));

end

%Учитывая правое граничное условие (65'),

%находим y(N) и далее вычисляем все решение y(i)

y(N)=(alpha(s)*p1(x(N))*d(N)+0.5*h^2*f(N))/...

(alpha(s)*p1(x(N))+0.5*h^2*(1+alpha(s)*...

p0(x(N)))-alpha(s)*p1(x(N))*c(N));

for i=N:-1:2

y(i-1)=c(i)*y(i)+d(i);

end

%Рисуем зашумленное решение f и сглаженное решение y

subplot(1,2,s); plot(x,f,x,y);

end

%Определяем функцию p0

function y=p0(x)

y=1+x^2;

%Определяем функцию p1

function y=p1(x)

y=1+x^2;

На рис.10 приведен итог работы кода программы листинга_№10. На левом рисунке представлена зашумленная функция f (x) и ее сглаженный вариант y_i, полученный с помощью метода сильной регуляризации, т.е. путем решения дифференциального уравнения (62) по разностным схемам (63), (65), (65¢). В качестве параметра регуляризации a выбиралось значение 10^-3. На правом рисунке представлены аналогичные профили, но при параметре регуляризации, равном 10^-4. Видно, что степень сглаживания на правом рисунке менее выражена по сравнению с аналогичным профилем на левом рисунке. Подбирая значение параметра регуляризации a можно добиться нужной степени сглаживания искомой функции.

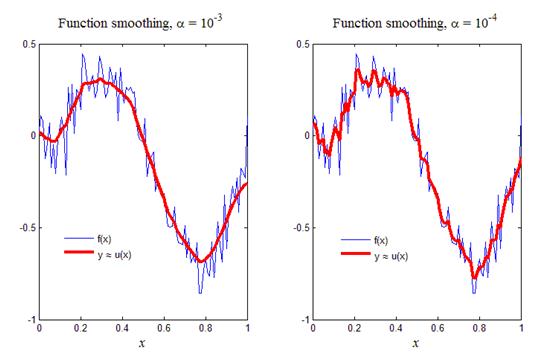
Рис.10. Сглаживание функции f (x) с помощью метода сильной
регуляризации путем численного решения уравнения (62)

Дифференцирование функции. Задачу дифференцирования u ¢(x) = f (x), x Î [ a, b ] можно представить в виде уравнения Вольтерра первого рода:

,

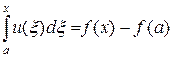которое в свою очередь может быть переписано в виде уравнения Фредгольма первого рода с разрывным ядром:

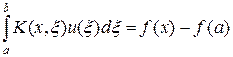, (66)

где

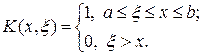(66¢)

Поскольку условие непрерывности ядра не является существенным, применим к данной задаче метод сильной регуляризации, тогда, учитывая (51¢), (66), (66¢), получим

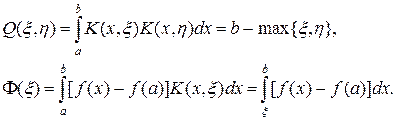(67)

Подставляя (67) в (51) и считая n = 1, получим следующее интегро-дифференциальное уравнение:

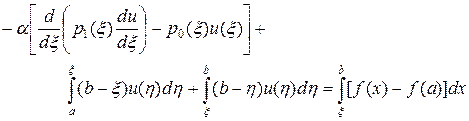(68)

плюс пара граничных условий .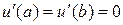

Для численного решения интегро-дифференциального уравнения (68) введем равномерные сетки по переменным x и h: x_i = a + h (i - 1), h_j = a + h (j - 1), i, j = 1,2,…, N, h = (b - a)/(N - 1). Аппроксимируем вторую производную в (68) симметричной второй разностью, а интегралы, входящие в левую часть уравнения, по формулам трапеции, тогда получим следующее разностное уравнение:

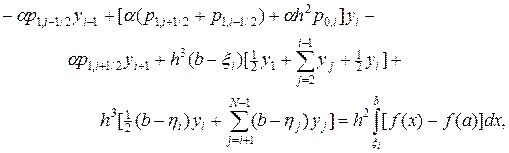(69)

где 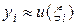, i = 2,…, N - 1. Следуя схеме предыдущего примера (64), аппроксимируем граничные условий u ¢(a) = u ¢(b) = 0 со вторым порядком точности по h, тогда левое и правое граничные условия предстанут в виде:

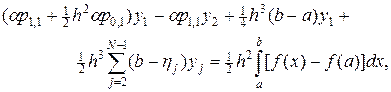(70)

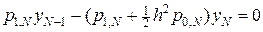. (70¢)

На листинге_№11 приведен код программы численного дифференцирования функции f (x) методом сильной регуляризации путем решения интегро-дифференциального уравнения (68) с помощью разностной схемы (69) — (70¢). Выбиралось следующее представление для функции f: f (x) = sin(px) + e (x), где e (x) — небольшая шумовая добавка. Численное решение y разностной задачи (69) — (70¢) сравнивалось с точным значением производной y_a = p cos(px) в рамках оценки ошибки error = || y - y_a || _C.

Листинг_№11

%Изучение процедуры численного дифференцирования

%функции f(x) с точки зрения метода регуляризации

%путем решения интегро-дифференциального уравнения

%(68) по разностной схеме (69), (70), (70')

function different

global a b N h f

%Определяем габариты области решения

a=0; b=1;

%Определяем число узлов и шаг разностной схемы

N=101; h=(b-a)/(N-1);

%Определяем сетки по xi и eta

xi=a:h:b; eta=a:h:b;

%Определяем функцию, производную которой

%необходимо найти

f=sin(pi*xi);

%Накладываем на функцию f(x) небольшое зашумление

for i=1:N

f(i)=f(i)+0.05*randn;

end

%Определяем производную незашумленной функции

ya=pi*cos(pi*xi);

%Рисуем толстой пунктирной линией производную

%незашумленной функции f(x)

subplot(1,2,1);

plot(xi,ya,'--','Color','red','LineWidth',4);

hold on

%Определяем перечень значений параметра регуляризации

alpha=[2e-4 1e-4 3e-5 1e-5 5e-6 2e-6];

%Организуем цикл расчетов с разными значениями

%параметра регуляризации

for s=1:length(alpha)

%Учитываем левое граничное условие (70)

A=zeros(N,N);

A(1,1)=alpha(s)*(p1(xi(1))+0.5*h^2*p0(xi(1)));

A(1,2)=-alpha(s)*p1(xi(1));

A(1,1)=A(1,1)+0.25*h^3*(b-a);

for j=2:(N-1)

A(1,j)=A(1,j)+0.5*h^3*(b-eta(j));

end

d(1)=0.5*h^2*fi(1);

%Учитываем разностную схему (69)

for i=2:(N-1)

A(i,i-1)=-alpha(s)*p1(xi(i)-0.5*h);

A(i,i)=alpha(s)*(p1(xi(i)+0.5*h)+...

p1(xi(i)-0.5*h)+h^2*p0(xi(i)));

A(i,i+1)=-alpha(s)*p1(xi(i)+0.5*h);

A(i,1)=A(i,1)+0.5*h^3*(b-xi(i));

if i>2

for j=2:(i-1)

A(i,j)=A(i,j)+h^3*(b-xi(i));

end

end

A(i,i)=A(i,i)+0.5*h^3*(b-xi(i));

A(i,i)=A(i,i)+0.5*h^3*(b-eta(i));

if i<(N-1)

for j=(i+1):(N-1)

A(i,j)=A(i,j)+h^3*(b-eta(j));

end

end

d(i)=h^2*fi(i);

end

%Учитываем правое граничное условие

A(N,N-1)=p1(xi(N));

A(N,N)=-p1(xi(N))-0.5*h^2*p0(xi(N));

d(N)=0;

%Решаем линейную систему уравнений Ay=d

y=A\d';

%Рисуем полученные численные производные

%зашумленной функции f(x) при различных

%значениях параметра регуляризации

subplot(1,2,1); plot(xi,y,'LineWidth',s/2.5);

hold on

%Оцениваем ошибку численного дифференцирования

%зашумленной функции в норме C

for i=1:N

z(i)=abs(y(i)-ya(i));

end

error(s)=max(z);

end

%Рисуем график зависимости ошибки численного

%дифференцирования методом регуляризации от

%параметра регуляризации

subplot(1,2,2); semilogx(alpha,error);

%Определяем функцию p0(xi)

function y=p0(xi)

y=1+xi;

%Определяем функцию p1(xi)

function y=p1(xi)

y=1+xi^2;

%Определяем функцию fi(xi(i)), которая

%определена в (67)

function y=fi(i)

global a b N h f

if i==N

y=0;

end

if i==(N-1)

y=0.5*h*(f(N-1)+f(N)-2*f(1));

end

if i<(N-1)

y=0.5*h*(f(i)+f(N)-2*f(1));

for j=(i+1):(N-1)

y=y+h*(f(j)-f(1));

end

end

На рис.11 приведен вариант работы кода программы листинга_№11. На левом рисунке приведены шесть профилей численного решения y, полученных при шести значениях параметра регуляризации a. Видно, что метод сильной регуляризации осуществляет процедуру дифференцирования корректно. Это выражается в сглаживании коротковолновых возмущений, привнесенных зашумленностью e (x). На правом рисунке приведен график зависимости ошибки численного решения от параметра регуляризации a. Видно, что параметр регуляризации имеет оптимальное значение a _opt, при котором ошибка является минимальной.

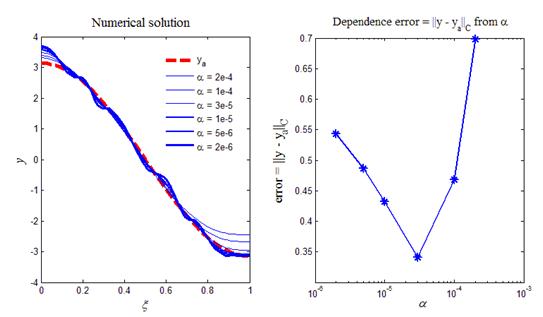
Рис.11. Изучение процедуры дифференцирования с помощью
метода сильной регуляризации (68) — (70¢)

[1] https://eqworld.ipmnet.ru/ru/solutions/ie/ie-toc6.htm

[2] Михлин С.Г. Лекции по линейным интегральным уравнениям. — М.: Физматгиз, 1959.

[3] https://eqworld.ipmnet.ru/en/solutions/ie/ie0402.pdf

[4] https://eqworld.ipmnet.ru/en/solutions/ie/ie0212.pdf

© Пространство C ^{( p )} — пространство функций u (x), a < x < b, непрерывных и ограниченных вместе со своими p -ми производными, причем.

[5] Калиткин Н.Н. Численные методы. — М.: Наука, Главн. ред. физ.-мат. литературы, 1978, с.471 — 473.