Рассмотрим в общих чертах процедуру моделирования равномерно распределенная случайная величина g. Выберем какое-либо устройство, на выходе которого могут появляться с равной вероятностью ½ две цифры 0 и 1. В качестве такого устройства можно выбрать монету, игральную кость (четно — 0, нечетно — 1) или специальный генератор, на основе подсчета числа (четно или нечетно) радиоактивных распадов, всплесков радиошума за определенное время и т.п.
Запишем g как двоичную дробь g = 0, a 1 a 2… и на место разрядов числа g после запятой поставим значения, которые выдает генератор, например, g = 0,0011001110101… Поскольку на первом месте после запятой 0 и 1 могут оказаться с равной вероятностью, постольку итоговое число может с равной вероятностью оказаться в левой и правой половинах единичного отрезка. Аналогично во втором разряде 0 и 1 могут оказаться с равной вероятностью, т.е. итоговое число может оказаться в одной из пары четвертей левой или пары четвертей правой половин и т.д. Таким образом, двоичная дробь со случайными цифрами 0 и 1 в разрядах действительно с равной вероятностью принимает любое значение на полуинтервале [0,1).
Реально моделируется только конечное количество разрядов k. По этой причине распределение будет не вполне равномерным. Так, математическое ожидание Mg окажется меньше ½ на величину ~2- k -1, т.к. значение g = 0 возможно, а g = 1 невозможно. Чтобы этот фактор не сказывался, достаточно брать случайные числа при достаточно большом числе разрядов k. Поскольку в методе статистических испытаний точность ответа обычно не превышает 0,1% = 10-3, то достаточно ограничиться условием 2- k < 10-3, что выполняется при k > 10. Последнее условие на современных компьютерах выполнено с большим запасом.
Псевдослучайные числа. Генераторы случайных чисел, основанные на тех или иных физических процессах, несвободны от различного рода систематических ошибок: несимметричность монеты, дрейф нуля в электронике и т.п. По этой причине качество выдаваемых ими случайных чисел проверяется различного рода специальными тестами.
Простейший тест состоит в вычислении для каждого разряда относительной частоты появления нуля (или единицы). Если относительная частота заметно отличается от ½, то имеется систематическая ошибка, если частота слишком близка к ½, то числа не случайные и есть какая-либо закономерность. Более сложные тесты сводятся к подсчету коэффициентов корреляции последовательных чисел
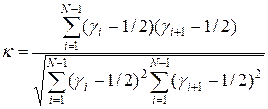 (3)
(3)
или групп разрядов в пределах одного числа. Все эти коэффициенты корреляции должны быть близки к нулю.
Если какая-либо последовательность чисел удовлетворяет данным тестам, то ее можно использовать в расчетах по методу Монте-Карло, не учитывая, каким способом она получена. Разработано огромное количество алгоритмов построения таких последовательностей. Символически эти алгоритмы можно представить в виде следующей рекуррентной зависимости:
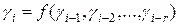 , (4)
, (4)
где r = 1,2,…
Числа, генерируемые согласно рекуррентному процессу (4) называются псевдослучайными. Для каждого алгоритма (4) есть свое предельное число членов последовательности, которое допустимо использовать в расчетах. При большем числе членов теряется случайность, например, числа начинают повторяться и последовательность становится периодической.
Применим данные тесты к генератору равномерно распределенных на отрезке [0,1] случайных чисел, представленному в MATLAB функцией rand. На листинге_№1 приведен код программы по тестированию генератора псевдослучайных чисел rand. Было запрограммировано два теста. Согласно первому тесту, в наборе случайных чисел формата 0, a 1 a 2…, представленных в десятичной форме записи, в k -м разряде подсчитывалась частота попадания числа в левую или правую половину отрезка [0,1]. Попадание в левую или правую половину отрезка определялось путем проверки выполнения или не выполнения неравенства ak £ 4. Согласно второму тесту, оценивался коэффициент корреляции k по формуле (3) между двумя подпоследовательностями { g 1, g 2,…, gN -1} и { g 2, g 3,…, gN } одной и той же последовательности { g 1, g 2,…, gN }.
Листинг_№1
%Тестирование генератора rand равномерно
%распределенных на отрезке [0,1] случайных чисел
clear all
%Определяем максимальную степень двойки nmax числа
%псевдослучайных чисел и номер разряда k, в котором
%будет подсчитано число попаданий чисел
%последовательности в левую или правую
%половину отрезка [0,1]
nmax=15; k=10;
%Организуем цикл расчетов с последовательностями
%псевдослучайных чисел разной длины
for n=1:nmax
%Определяем длину последовательности
%псевдослучайных чисел, как степень двойки
N=2^n;
%Генерируем с помощью функции rand
%последовательность чисел длины N
gamma=rand(1,N);
%Тест №1
%Определяем счетчики числа попаданий в левую cl и
%правую половины cr отрезка [0,1]
cl=0; cr=0;
for i=1:N
%Выделяем k-й разряд случайного числа
g=10^k*gamma(i);
g=mod(g,10);
s=g-mod(g,1);
if s<=4
cl=cl+1;
else
cr=cr+1;
end
end
%Запоминаем число попаданий в левую и правую
%половины отрезка [0,1]
frl(n)=cl/N; frr(n)=cr/N;
%Тест №2
%Определяем две подпоследовательности
%gamma1 и gamma2
for i=1:(N-1)
gamma1(i)=gamma(i);
gamma2(i)=gamma(i+1);
end
%Вычисляем коэффициент корреляции kappa между
%парой подпоследовательностей
covar=0; s1=0; s2=0;
for i=1:(N-1)
covar=covar+(gamma1(i)-0.5)*(gamma2(i)-0.5);
s1=s1+(gamma1(i)-0.5)^2;
s2=s2+(gamma2(i)-0.5)^2;
end
kappa(n)=covar/sqrt(s1*s2);
lng(n)=N;
end
%Рисуем график числа попаданий в левую и правую
%половины отрезка [0,1] в к-м разряде от длины
%последовательности чисел lng
subplot(1,2,1); semilogx(lng,frl,lng,frr,'--');
%Рисуем график коэффициента корреляции от длины
%последовательности случайных чисел lng
subplot(1,2,2); loglog(lng,abs(kappa));
На рис.1 приведен итог работы кода программы листинга_№1. На левом рисунке представлены два графика частоты попадания k -го разряда в левую или правую половину отрезка [0,1]. В расчете выбирался десятый разряд, т.е. k =10. Видно, что, по мере увеличения длины последовательности псевдослучайных чисел, частоты стремятся к предельному значению ½. На правом рисунке представлена зависимость коэффициента корреляции от длины последовательности псевдослучайных чисел. Видно, что, по мере роста длины последовательности, коэффициент корреляции в среднем уменьшается и стремится к нулю.
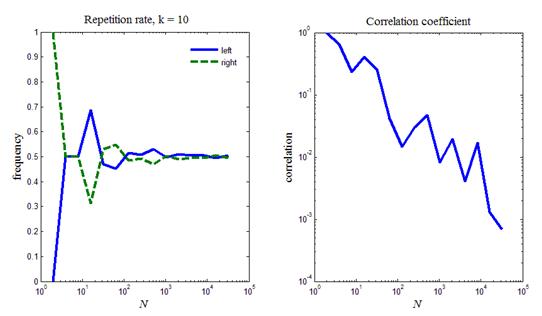
Рис.1. Тестирование MATLAB датчика псевдослучайных чисел rand
Наиболее употребителен алгоритм, связанный с выделением дробной части произведения
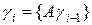 , (5)
, (5)
где {,} — функция возврата дробной части числа, A — считается очень большой константой. Качество псевдослучайных чисел сильно зависит от выбора числа A, в двоичной записи оно должно иметь достаточно случайный вид. Величина начального приближения g 0 слабо влияет на последовательность псевдослучайных чисел, хотя и находятся такие g 0, которые приводят к неудовлетворительным последовательностям. В таблице ниже приведены некоторые ранее апробированные значения параметров A и g 0.
| Некоторые значения параметров генератора псевдослучайных чисел (5) | |||
| A | 513 | 517 | 517 |
| g 0 | 2-36 | 2-40 | 2-42 |
На листинге_№2 приведен код программы тестирования датчика псевдослучайных чисел (5) при двух значениях параметров A и g 0.
Листинг_№2
%Тестирование простейших датчиков псевдослучайных
%чисел (5) при различных значениях констант A и gamma0
clear all
%Определяем длину последовательности псевдослучайных
%чисел
N=10^4;
%Задаем значения констант A и gamma0
A=[5^13 170]; gamma0=[2^(-36) 0.01];
%Организуем цикл расчетов с различными значениями
%констант A и gamma0
for s=1:length(A)
%Генерируем последовательность псевдослучайных
%чисел, согласно алгоритму (5)
gamma(1)=mod(A(s)*gamma0(s),1);
for i=2:N
gamma(i)=mod(A(s)*gamma(i-1),1);
end
%Строим точечную диаграмму в координатах gamma(i-1)
%и gamma(i) соответственно
subplot(1,2,s);
plot(gamma([1:(N-1)]),gamma([2:N]),'.');
%Тест №1
%Определяем счетчики числа попаданий в левую cl и
%правую половины cr отрезка [0,1] в к-ом разряде
k=10; cl=0; cr=0;
for i=1:N
%Выделяем k-й разряд случайного числа
g=10^k*gamma(i);
g=mod(g,10);
s=g-mod(g,1);
if s<=4
cl=cl+1;
else
cr=cr+1;
end
end
%Запоминаем число попаданий в левую и правую
%половины отрезка [0,1]
frl=cl/N; frr=cr/N;
%Тест №2
%Определяем две подпоследовательности
%gamma1 и gamma2
for i=1:(N-1)
gamma1(i)=gamma(i);
gamma2(i)=gamma(i+1);
end
%Вычисляем коэффициент корреляции kappa между
%парой подпоследовательностей
covar=0; s1=0; s2=0;
for i=1:(N-1)
covar=covar+(gamma1(i)-0.5)*(gamma2(i)-0.5);
s1=s1+(gamma1(i)-0.5)^2;
s2=s2+(gamma2(i)-0.5)^2;
end
kappa=covar/sqrt(s1*s2);
%Выводим при выбранных значениях констант A и gamma0
%число попаданий в левую и правую половины отрезка [0,1]
%в k-ом разряде, а также коэффициент корреляции kappa
[frl frr kappa]
end
Код программы листинга_№2 генерирует два графика — две точечные диаграммы в координатах 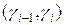 , представленных на рис.2. На левой диаграмме точки плотно покрывают единичный квадрат, что говорит о хорошем качестве данного набора псевдослучайных чисел. На правом графике имеет место зацикливание процесса (gi = 0 при i > 47), точки не могут плотно покрыть единичный квадрат, что говорит о плохом качестве псевдослучайных чисел при выборе параметров A = 170 и g 0 = 0.01.
, представленных на рис.2. На левой диаграмме точки плотно покрывают единичный квадрат, что говорит о хорошем качестве данного набора псевдослучайных чисел. На правом графике имеет место зацикливание процесса (gi = 0 при i > 47), точки не могут плотно покрыть единичный квадрат, что говорит о плохом качестве псевдослучайных чисел при выборе параметров A = 170 и g 0 = 0.01.
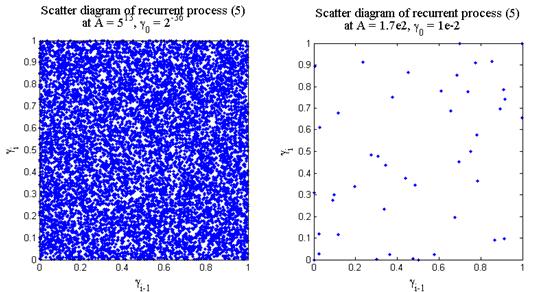
Рис.2. Точечные диаграммы рекуррентных алгоритмов (5) при
двух различных парах параметров A и g 0
Кроме диаграмм рассеяния, представленных на рис.2, код программы листинга_№2 возвращает частоты попадания десятого разряда псевдослучайных чисел в левую и правую половины отрезка [0,1], а также коэффициент корреляции, вычисленный согласно формуле (3). Ниже представлены соответствующие численные значения обоих тестов для двух пар параметров A и g 0:
A = 513, g 0 = 2-36:
0.50100000000000 0.49900000000000 -0.00450974364702
A = 170, g 0 = 0.01:
0.99780000000000 0.00220000000000 0.99885276017610
Анализ этих данных показывает, что набор псевдослучайных чисел, полученный в соответствии с первой парой значений A = 513, g 0 = 2-36, удовлетворяет обоим тестам. Вторая пара значений параметров A = 170, g 0 = 0.01 приводит к набору чисел, которые не удовлетворяют ни первому (превалирует попадание десятого разряда в левую половину отрезка [0,1]), ни второму тестам (коэффициент корреляции близок к единице).
Произвольное распределение. Для разыгрывания случайной величины с неравномерным распределением r (x) воспользуемся формулой (2). Выберем случайным образом gi и найдем xi из уравнения
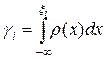 . (6)
. (6)
В качестве примера рассмотрим распределение с 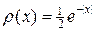 . В этом случае уравнение (6) легко решается и находится ответ:
. В этом случае уравнение (6) легко решается и находится ответ:
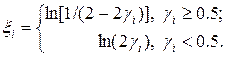 (7)
(7)
На листинге_№3 приведен код программы, которая разыгрывает случайные величины xi с законом распределения 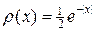 .
.
Листинг_№3
%Разыгрывание случайной величины xi,
%распределенной по закону 0.5*exp(-abs(x))
%согласно формуле (7)
clear all
%Определяем длину последовательности
N=10^4;
%Организуем цикл генерации последовательности
%псевдослучайных чисел с законом распределения
%0.5*exp(-abs(x))
for i=1:N
gamma=rand;
if gamma>=0.5
xi(i)=log(1.0/(2-2*gamma));
else
xi(i)=log(2*gamma);
end
end
x=-10:0.05:10;
%Рисуем гистограмму совокупности чисел xi
hist(xi,x);
Итогом работы кода программы листинга_№3 является гистограмма, моделирующая плотность распределения полученной совокупности псевдослучайных чисел. На гистограмме по оси ординат отложено число членов из исходной совокупности, которые попадают в определенный интервал оси абсцисс. Интервал определяется массивом x в программе листинга_№3. Визуально видна схожесть гистограммы и графика функции плотности распределения 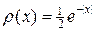 .
.
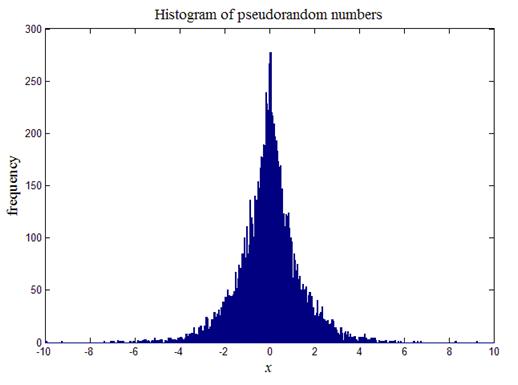
Рис.3. Гистограмма распределения псевдослучайных чисел,
построенных согласно формуле (7)
 2014-02-09
2014-02-09 820
820








