Сходимость

Рассмотрим дифференциальное уравнение с граничными условиями

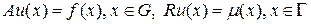. (83)

Для задачи (83) определим аппроксимирующую ее разностную схему на сетке, состоящей из регулярных и нерегулярных узлов w_h, g_h соответственно:

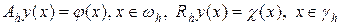. (84)

Для изучения вопроса о сходимости нас будет интересовать близость разностного решения y (x) и точного решения u (x) на сетке w_h + g_h, при этом для сравнения естественно использовать одну из сеточных норм.

Определение. Разностное решение y (x) задачи (84) сходится к решению u (x) дифференциальной задачи (83), если

;

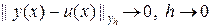разностное решение имеет порядок точности p, если

.

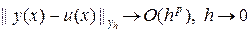Определение. Разностная задача (84) корректна, если ее решение существует и единственно при любых входных данных j и c из соответствующих классов и схема устойчива.

Теорема [6]. Если решение u (x) задачи (83) существует, разностная схема (84) корректна и аппроксимирует задачу (83) на данном решении, то разностное решение сходится к точному.

Доказательство. Запишем цепочку преобразований:

,

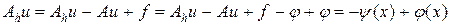где y (x) — невязка разностной схемы. Проводя аналогичные преобразования для граничных условий, получим

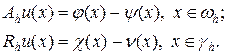(85)

Сравнивая (84) и (85), можно увидеть, что уравнения (85) являются разностными уравнениями (84) с модифицированной за счет невязки правой частью.

Поскольку разностная схема устойчива, постольку для любого e > 0 найдется такое d (e), что 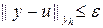, есл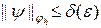и и .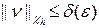

По определению аппроксимации для любого d > 0 найдется такое h ₀(d), что 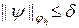и при h £ h ₀(d).

Таким образом, для любого e > 0 найдется такое h ₀(d (e)), что 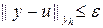при h £ h ₀(d (e)), т.е. имеет место сходимость. Теорема доказана.

[1] Плохотников К.Э. Математическое моделирование и вычислительный эксперимент. Методология и практика. — М.: Едиториал УРСС. 2003.

[2] Тихонов А.Н., Самарский А.А. Уравнения математической физики. — М.: Наука, Гл. ред. физ.-мат. литературы, 1972; Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. — М.: Высшая школа, 1970.

[3] Режимы с обострением. Эволюция идеи: Законы коэволюции сложных структур/ Сб. статей/ Ред. Г.Г. Малинецкий/ Кибернетика: неограниченные возможности и возможные ограничения. — М.: Наука, 1999. 255с.

© Из локальной близости функций следует их среднеквадратическая близость, поэтому ||·||_C называют более сильной, чем.

[4] Определение понятия устойчивости, обозначения и доказательства теорем с некоторыми модификациями заимствованы из учебного пособия: Калиткин Н.Н. Численные методы. — М.: Наука, Главная ред. физ.-мат. лит., 1978.

[5] Самарский А.А. Теория разностных схем. — М.: Наука, Главн. ред. физ.-мат. литературы, 1977.

[6] Данная теорема кратко еще формулируется таким образом: “Из аппроксимации и устойчивости следует сходимость”.