Применение метода укороченных уравнений для исследования автогенератора гармонических колебаний

В режиме большого сигнала уже нельзя пренебречь нелинейностью характеристики электронного прибора. Исследование основано на приближенном интегрировании нелинейного дифференциального уравнения автогенератора. Для автогенератора с трансформаторной связью можно использовать нелинейную систему, полученную в п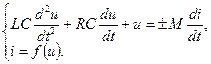. 5.3:

(5.3)

Нелинейное уравнение автогенератора получим подстановкой второго уравнения системы (5.3) (ВАХ нелинейного прибора) в первое из уравнений. Учтем, что 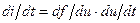. В правой части первого из уравнений системы (5.3) выберем знак 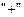, отвечающий положительной обратной связи в автогенераторе. Получим искомое нелинейное уравнение автогенератора:

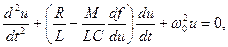(5.46)

где 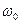- резонансная частота высокодобротного колебательного контура в генераторе, .

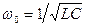Даже при наличии нелинейного элемента напряжение на колебательном контуре мало отличается от гармонического с частотой 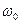ввиду высокой добротности этого контура.

Метод укороченного уравнения. Ищем приближенное решение уравнения (5.46) в виде: 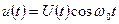, где амплитуда 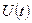медленно изменяется со временем так, что 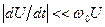. Тогда первая производная

.

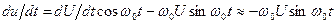Аналогично вторая производная

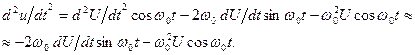
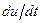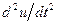Эти приближенные выражения для и подставим в (5.46), получим укороченное дифференциальное уравнение

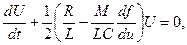(5.47)

описывающее приближенно процессы в автогенераторе с высокодобротным колебательным контуром.

Применение (5.47) вместо (5.46) понижает порядок уравнения на единицу и упрощает анализ.

Средняя крутизна. Производная 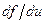, входящая в (5.47), - дифференциальная проводимость нелинейного элемента. Ток 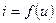- периодическая функция, которую можно разложить в ряд Фурье: 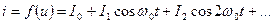. Возьмем в качестве функции 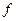не весь ток 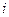, а сумму тока первой гармоники и постоянной составляющей (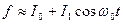). В том же приближении напряжение 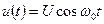является гармоническим. Тогда

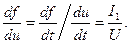
Определение. Коэффициент пропорциональности между амплитудой первой гармоники тока и амплитудой напряжения на управляющем электроде нелинейного элемента называется средней крутизной или крутизной по первой гармонике:

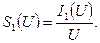(5.48)

По графику колебательной характеристики 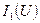нелинейного элемента среднюю крутизну 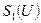можно найти как тангенс угла наклона прямой, проходящей через начало системы координат и точку 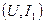на графике колебательной характеристики, к оси 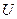. Для аналитического определения колебательной характеристики можно использовать формулу преобразования Фурье:

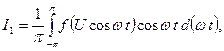
где ВАХ нелинейного элемента аппроксимирована относительно смещения в рабочей точке, а для определения средней крутизны достаточно подставить это выражение в (5.48).

В (5.47) приближенно подставим в качестве значения крутизны 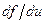среднюю крутизну из (5.48):

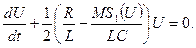(5.49)

Для аналитического рассмотрения удобен случай, когда ВАХ нелинейного элемента имеет вид степенного ряда: 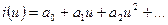, где 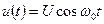. Эту функцию разложим в ряд Фурье 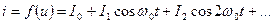. В частности, получим 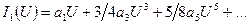, отсюда

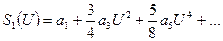(5.50)

Подставим (5.50) в (5.49), получим нелинейное дифференциальное уравнение первого порядка, которое далее можно решать методом разделения переменных.

Стационарный режим автогенератора. В стационарном режиме, по определению, амплитуда 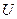выходного напряжения автогенератора постоянна, то есть 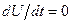. Тогда из (5.49) получаем уравнение:

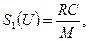(5.51)

положительные корни которого определяют стационарные значения 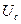амплитуды автоколебаний.

Пример. Пусть средняя крутизна активного элемента автогенератора 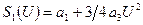, где 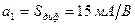, 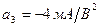. Параметры автогенератора: 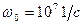, , 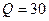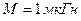. Найдем стационарную амплитуду автоколебаний.

Сначала найдем 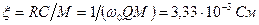. Уравнение (5.51) принимает вид: 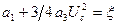. Решив его, найдем амплитуду стационарных автоколебаний: .

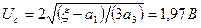В зависимости от того, в какой области ВАХ расположена рабочая точка нелинейного элемента, характеристика 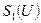имеет одну из двух форм (см. рис. 5.23).

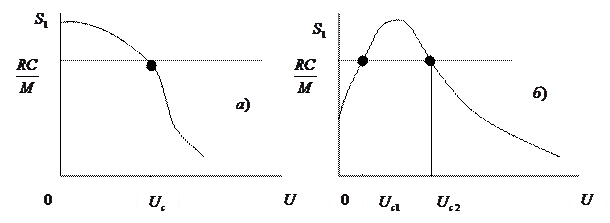Рис. 5.23

Мягкому режиму самовозбуждения автогенератора соответствует случай 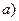на рис. 5.23, когда средняя крутизна монотонно убывает с увеличением амплитуды управляющего напряжения 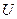. Горизонтальная прямая с ординатой 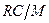называется прямой обратной связи. Точка пересечения этой прямой с кривой 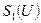характеристики мягкого режима самовозбуждения определяет единственную возможную в данном случае амплитуду 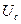стационарных колебаний.

Жесткому режиму самовозбуждения автогенератора соответствует случай рис. 5.23, б. Здесь могут быть два стационарных режима с различными амплитудам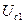и и 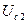на пересечении прямой обратной связи с кривой 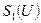характеристики жесткого режима самовозбуждения.

Устойчивость стационарных режимов. По определению, стационарный режим автоколебательной системы устойчив, если при малых отклонениях амплитуды гармонических колебаний от стационарного значения система стремится вернуться в то же стационарное состояние. Если же система при этом стремится изменить свою амплитуду так, чтобы перейти к новому стационарному состоянию, то стационарное состояние неустойчиво. Для линейной динамической системы в режиме малых колебаний может быть устойчивым или неустойчивым только состояние покоя. Напротив, для нелинейной системы устойчивым или неустойчивым может быть также и стационарное состояние. Пусть амплитуда 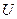автоколебаний получила малое отклонение 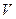от стационарного значения :

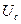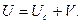(5.52)

При этом

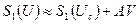, (5.53)

где 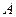- тангенс угла наклона средней крутизны к оси напряжения 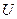в стационарной точке, .

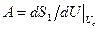Подставим (5.52) и (5.53) в (5.49). С учетом (5.51) получим дифференциальное уравнение относительно возмущения амплитуды:

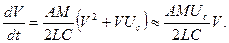(5.54)

В (5.54) знак производной 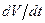зависит лишь от знака величины 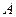. Если 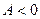, то знак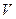и и 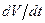противоположны. Если в силу действия каких-то причин, например, - флуктуаций, оказалось, что амплитуда 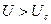(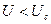), то есть 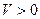(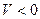), то, согласно (5.54), 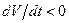(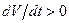). Значит, отклонение системы из стационарного состояния вызывает противодействие, стремящееся вернуть систему в это состояние. Такое стационарное состояние устойчиво.

На рис. 5.24, а 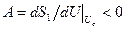на кривой 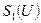характеристики мягкого режима самовозбуждения. В случае прямой 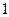(при достаточно малом значении коэффициента взаимной индукции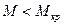, где 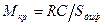) может реализоваться единственно возможное устойчивое состояние – состояние покоя, когда амплитуда колебаний равна нулю. При критическом уровне связи контуров (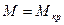, прямая 2) самовозбуждение автогенератора возможно, но с бесконечно малой амплитудой колебаний в установившемся режиме. Дальнейшее увеличение 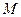приводит к увеличению амплитуды колебаний устойчивого стационарного режима.

Вывод: Мягкий режим самовозбуждения колебаний характеризуется плавной зависимостью амплитуды автоколебаний от величины обратной связи.

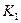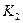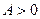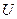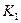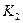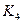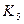На рис. 5.24, б, соответствующем характеристике жесткого режима самовозбуждения, в точках и имеем: (крутизна характеристики возрастает с ростом ). Соответственно, и - состояние покоя и стационарное состояние с ненулевой амплитудой (оба неустойчивые). Аналогично, и - устойчивые стационарные состояния с ненулевыми амплитудами. Например, при значении 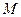, соответствующем положению 1, из состояния покоя колебания самовозбудиться не могут. Но если внешним воздействием возбудить в системе колебания с амплитудой, близкой к той, которая соответствует состоянию 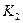(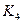) на резонансной частоте 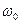, то колебания будут неустойчивые (колебания выйдут на стационарный режим 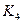). Автогенератор с характеристикой рис. 5.24, б все же способен к самовозбуждению. Для этого, изменяя значение 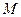, надо реализовать положение 2. Из неустойчивого состояния покоя система в конце концов переходит в устойчивое стационарное состояние с амплитудой 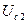. Если значение 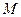теперь плавно уменьшать, то амплитуда стационарных колебаний будет становиться все меньше, пока не достигнет значения 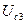. Дальнейшее уменьшение значения 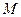приводит к скачкообразному срыву генерации стационарных автоколебаний, когда амплитуда колебаний падает до нуля.

Вывод: Жесткий режим самовозбуждения колебаний характеризуется скачкообразным возникновением колебаний при плавном увеличении обратной связи и скачкообразным срывом колебаний при меньшей обратной связи.

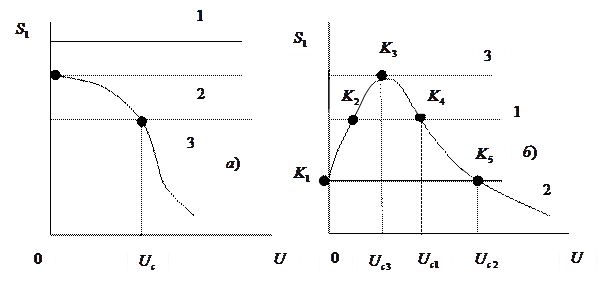Рис. 5.24

Видно, что в автогенераторе с жестким режимом самовозбуждения стационарные колебания возникают и исчезают при разных значениях 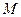. Об этом свойстве говорят, как о колебательном гистерезисе.

Зависимость режима автогенератора от выбора рабочей точки. ВАХ нелинейного элемента выразим степенным рядом. 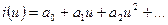. В соответствии с (5.50) при малых значениях амплитуды 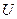используем квадратичную аппроксимацию средней крутизны ВАХ:

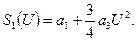(5.55)

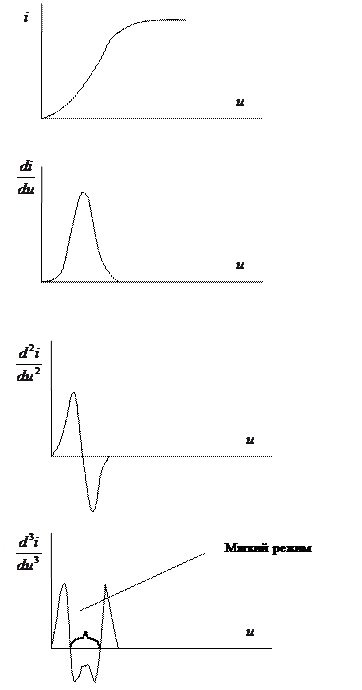
Рис. 5.25. Определение границ мягкого и жесткого режимов самовозбуждения

Мягкий режим самовозбуждения от жесткого отличается тем, что при малых значениях амплитуды 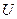напряжения средняя крутизна 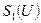отрицательна, а не положительна. Значит, автогенератор работает в мягком (жестком) режиме самовозбуждения, если 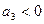(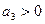). Производная 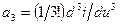берется в рабочей точке, определяемой постоянным смещением. Типичное поведение ВАХ нелинейного элемента (лампы или транзистора) показано на рис. 5.25. Видно, что мягкий режим реализуется, если рабочая точка выбрана в средней части ВАХ. Анализ графика ВАХ позволяет сделать следующий вывод.

Вывод. При анализе работы генератора в мягком режиме ВАХ его нелинейного элемента должна быть аппроксимирована полиномом не ниже третьей степени, а в жестком режиме – не ниже пятой степени.

Процесс установления стационарной амплитуды. Выше метод укороченного уравнения был применен для нахождения стационарных режимов автоколебаний и изучения их устойчивости. Его также можно применить и для изучения процесса установления стационарной амплитуды колебаний. Рассмотрим автогенератор с мягким режимом самовозбуждения. Пусть при 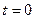в системе существуют гармонические колебания на резонансной частоте с некоторой амплитудой 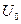. Найдем закон 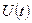изменения амплитуды со временем при 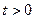. Подставим (5.55) в (5.49), получим уравнение

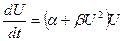(5.56)

с начальным условием 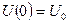, где , .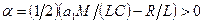

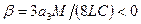Умножим (5.56) на 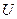, получим

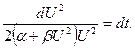(5.57)

Левую часть в (5.57) разложим на элементарные дроби, интегрируем полученное уравнение. Для определения константы интегрирования применим заданное начальное условие. Получим результат:

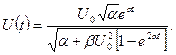(5.58)

При 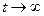амплитуда автоколебаний стремится к стационарному значению:

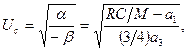(5.59)

что совпадает с выводом, полученным выше в примере.

Стационарная амплитуда колебаний не зависит от начальных условий. Если 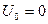, то 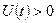при любых 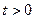.Так как 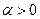, то режим малых по амплитуде колебаний - неустойчивый при любой сколь угодно малой величине начальной амплитуды 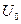колебаний, возникающих первоначально, например, из-за тепловых флуктуаций. Самовозбуждение, значит, всегда возможно. С увеличением добротности колебательной системы генератора (при 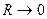) параметр увеличивается. Согласно (5.58), установление стационарной амплитуды происходит тем быстрее, чем больше , то есть - добротность колебательной системы. Заметим, что в пассивных резонансных системах при установлении колебаний огибающая меняется тем медленнее, чем больше добротность системы.