Рассмотрим разложение светового поля в ряд Фурье в выражении для интенсивности света
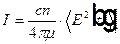 =
= 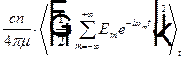 =
= 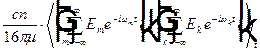 =
= 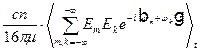
Последняя сумма состоит из слагаемых, осциллирующих на частотах 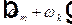 . Если эта частота не равна нулю, то при усреднении по времени слагаемое обращается в нуль. Следовательно, отличны от нуля только слагаемые, для которых выполнено условие
. Если эта частота не равна нулю, то при усреднении по времени слагаемое обращается в нуль. Следовательно, отличны от нуля только слагаемые, для которых выполнено условие 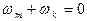 , что справедливо только при
, что справедливо только при 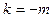 . Тогда в выражении для интенсивности вместо двойной суммы остается одинарная сумма, в которой слагаемые не осциллируют и не нуждаются в усреднении по времени.
. Тогда в выражении для интенсивности вместо двойной суммы остается одинарная сумма, в которой слагаемые не осциллируют и не нуждаются в усреднении по времени.
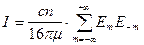 =
= 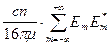 =
= 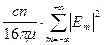 =
= 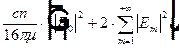 =
= 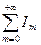 .
.
Окончательно получаем
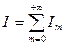 ,
,
что означает, что интенсивность света равна сумме интенсивностей волн на составляющих частотах. Здесь введены обозначения
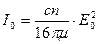 и
и
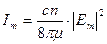 при
при 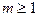 .
.
Если в разложении присутствует только одна частота, то выражение 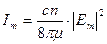 — это обычная связь интенсивности света и комплексной амплитуды световой волны на частоте
— это обычная связь интенсивности света и комплексной амплитуды световой волны на частоте 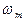 .
.
В случае непрерывного спектра аналогичные формулы будут иметь вид
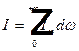 , где
, где
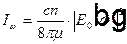
Величина 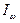 называется спектральной плотностью интенсивности света или просто спектром света. Обратите внимание, что спектром света называют спектральную плотность интенсивности
называется спектральной плотностью интенсивности света или просто спектром света. Обратите внимание, что спектром света называют спектральную плотность интенсивности 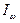 , а не Фурье образ светового поля
, а не Фурье образ светового поля 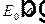 .
.
 2014-02-10
2014-02-10 495
495








